荷载集度、剪力、弯矩之间的微分关系

通过上节例题发现,用方程法绘制梁的内力图需要借助于方程,略显烦琐。尤其是在梁上荷载分布比较复杂,导致内力方程是分段函数的情况下,更为烦琐。既然荷载与内力方程直接相关,由内力方程可以画出内力图,那么它们之间应该有某些更显见、简洁的关系,因此找到荷载、内力方程间以及内力图之间的这种关系,并利用这种关系绕过内力方程便可直接绘制内力图。

在上节例8.9中,梁的剪力方程和弯矩方程分别为

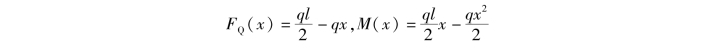
若将剪力方程和弯矩方程分别对x求导数,则正好等于均布荷载集度和剪力方程。若设q(x)为分布荷载集度,且向上为正,则一般地:

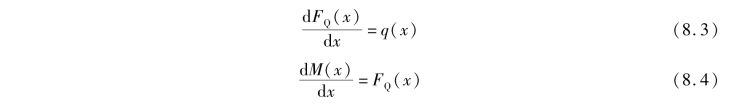
由上两式还可得到

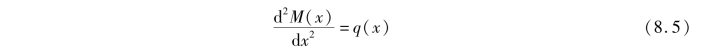
以上三式就是剪力、弯矩与分布荷载集度之间的微分关系。

下面总结内力图与荷载、内力方程间一些显而易见的图形特征。根据式(8.3)—式(8.5),可得出剪力图和弯矩图的如下特征和规律:

①在无荷载作用区段,q(x)=0。由可知,FQ(x)是常数,故剪力图必为平行于x轴的直线,称为平直线。又因常数可知,弯矩M(x)为x的一次函数,故弯矩图必为斜直线,其倾斜方向由剪力正负值决定:

当FQ(x)>0时,弯矩图为增函数图像,因此斜向右下方;

当FQ(x)<0时,弯矩图为减函数图像,因此斜向右上方;(www.xing528.com)

当FQ(x)=0时,弯矩图为水平直线。

②在均布荷载作用的区段,q(x)=常数≠0,由常数可知,该梁段FQ(x)为x的一次函数,而弯矩M(x)为x的二次函数,故剪力图是斜直线,而弯矩图是抛物线。

当q(x)>0(荷载向上)时,剪力图为向上倾斜的直线,弯矩图为向上凸的抛物线;

当q(x)<0(荷载向下)时,剪力图为向下倾斜的直线,弯矩图为向下凸的抛物线。

③弯矩的极值:由可知,若某截面上的剪力FQ(x)=0,则该截面上的弯矩M(x)必为极值。

④在集中力作用处剪力图上出现突变;在集中力偶作用处弯矩图上出现突变。

为了方便使用,现将以上规律和剪力图、弯矩图的特征用表8.1的形式加以表述,供参考。

表8.1　FQ,M图特征表

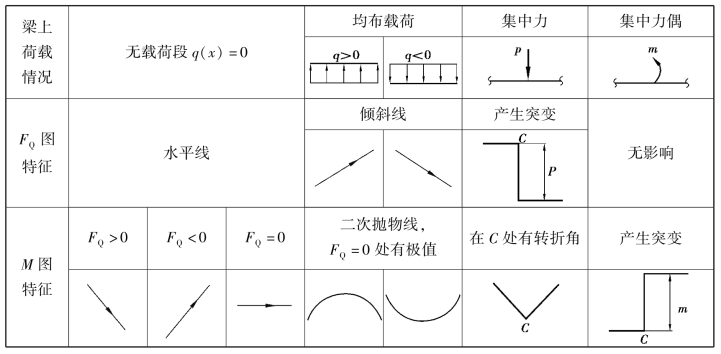
结合内力方程记住上述内力图特征,将有利于本课程的学习。利用表8.1中的特征与控制截面相结合,可以快速、准确地绘制出剪力图和弯矩图,从而避开内力方程的求解。