《建筑力学（第2版）》3节：截面法求剪力和弯矩

现以如图8.9(a)所示的简支梁为例,求其任一横截面m—m上的内力。

首先,对整体AB梁建立平衡方程,求解梁的支座反力〔图8.9(b)〕。

其次,将梁在m—m截面处假想地截开,成为左、右两段,截面左右两部分梁仍应处于平衡态。任选一段,例如取左段作为研究对象〔图8.9(c)〕,要保持该部分梁的平衡状态,截面上必定有一个作用线与FAy平行而指向与FAy相反的内力,设此内力为FQ。对该左段梁建立平衡方程

图8.9

以横截面m—m的形心O为矩心,对该段梁建立力矩平衡方程,由

由于右段为研究对象,同样可以求得横截面m—m上的内力FQ和M〔图8.9(d)〕。

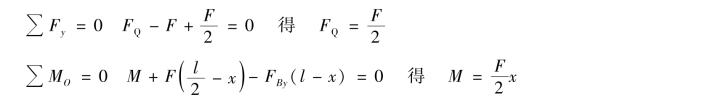
两者大小相等、方向相反。正负符号相同,物理性质相同。

由上面的叙述可以得出求横截面上的方法如下:

欲求内力,先求外力;假想切开,弃去一半;代之以力,平衡求解。

在用截面法计算梁的弯曲内力时要注意的几点:

①在用截面法求弯曲内力时,剪力、弯矩的方向一般按正方向假设,以免引起计算混乱。

②从弯曲内力的运算结果要能判断出梁的变形情况。如剪力的运算结果为正,说明梁在该截面处产生左上右下错动的剪切变形;如弯矩的运算结果为正,说明梁在该截面处下边缘纤维受拉,上边缘纤维受压。

【例8.1】　简支梁如图8.10(a)所示。求横截面1—1,2—2,3—3上的剪力和弯矩。

【解】　①求支座反力。由梁的支承及荷载分布的对称性,根据平衡方程求得支座A,B处的反力为

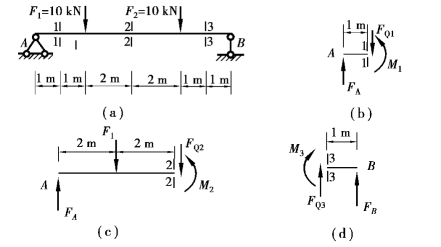
图8.10(www.xing528.com)

②求横截面1—1上的剪力和弯矩。假想地沿横截面1—1把梁截开成两段,因左段梁受力较简单,故取它为研究对象,并设横截面上的剪力FQ1和弯矩M1均为正〔图8.10(b)〕。列出平衡方程

得

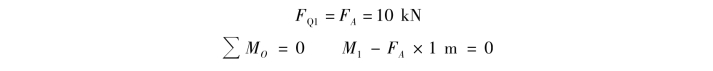
得

计算结果FQ1与M1为正,表明两者的实际方向与假设相同,即FQ1为正剪力,M1为正弯矩。

③求横截面2—2上的剪力和弯矩。假想地沿横截面2—2把梁截开,仍取左段梁为研究对象,设横截面上的剪力FQ2和弯矩M2均为正〔图8.10(c)〕。由平衡方程

得

得

由计算结果知,M2为正弯矩。

④求横截面3—3上的剪力和弯矩。假想地沿横截面3—3把梁截开,取右段梁为研究对象,设横截面上的剪力FQ3和弯矩M3均为正〔图8.10(d)〕。由平衡方程

得

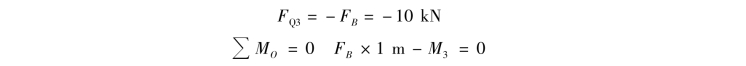
得

计算结果FQ3为负,表明FQ3的实际方向与假设相反,即FQ3为负剪力,M3为正弯矩。