建筑力学第2版：体系几何组成分析举例

几何不变体系的组成规则是进行几何组成分析的依据。规则本身是简单浅显的,但规则的应用则变化无穷,因此本章的难点在于规则的应用。要由浅入深地做必要的练习,逐步提高运用能力,以达到灵活运用这些规则,判定体系是否是几何不变体系及有无多余约束等。

体系的几何组成分析方法是灵活多样的,但也不是无规律可循。一般分析步骤如下:

①选择刚片。在体系中任选杆件或某个几何不变的部分(例如基础、铰接三角形)作为刚片。在选择刚片时,要考虑哪些是连接这些刚片的约束,然后利用三刚片或两刚片规则。当分析进行不下去时,大多是由于所选的刚片不恰当造成的,应重新调整思路(扩大刚片或选择其他作为刚片)再进行试分析。

②先从能直接观察到的几何不变部分开始,应用几何组成规则,逐步扩大几何不变部分直至整体。

③对于复杂体系可以采用以下方法简化体系:

a.当体系上有二元体时,应采用减法,依次拆除二元体。

b.如果体系只用三根不全互于一点也不全平行的支座链杆与基础相连,则可以拆除支座链杆与基础,只分析上部体系。

c.利用等效替换。例如:只有两个铰与其他部分相连的刚片可用直链杆代替;连接两个刚片的两根链杆可用其互点处的虚铰代替。

【例7.1】　试对如图7.17所示体系进行几何组成分析。

图7.17

【解】　在此体系中,将基础视为刚片,AB杆视为刚片,两个刚片用三根不全交于一点也不全平行的链杆1,2,3相连,根据两刚片规则,此部分组成几何不变体系,且没有多余约束。然后将其视为一个大刚片,它与BC杆再用铰B和不通过该铰的链杆4相连,又组成几何不变体系,且没有多余约束。因此,整个体系为几何不变的,且无多余约束。

【例7.2】　试对如图7.18所示体系进行几何组成分析。

图7.18

【解】　体系中ADC部分是由铰接三角形AFG逐次加上二元体所组成,是一个几何不变部分,可视为刚片I。同样,BEC部分也是几何不变,可视为刚片Ⅱ。再将基础视为刚片Ⅲ,固定铰支座A,B相当于两个铰,则三个刚片由三个不共线的铰A,B,C两两相连,该体系为几何不变的,且无多余约束。

【例7.3】　试对如图7.19所示体系进行几何组成分析。

【解】　在此体系中,ABCD部分是由一个铰接三角形增加一个二元体组成的几何不变部分,视为刚片Ⅰ;同理,CEFG部分也是几何不变部分,视为刚片Ⅱ。再将基础看成刚片,并以Ⅲ表示。刚片Ⅰ和Ⅱ用铰C连接,刚片Ⅰ和Ⅲ用链杆1、2构成的虚铰O1连接,刚片Ⅱ和Ⅲ用链杆3、4构成的虚铰O2连接,由于铰C和虚铰O1、O2不在同一直线上,所以此体系为几何不变的,且无多余约束。

【例7.4】　试对如图7.20所示体系进行几何组成分析。(www.xing528.com)

图7.19

图7.20

【解】　在此体系中,刚片AC只有两个铰与其他部分相连,其作用相当于一根用虚线表示的链杆1。同理,刚片BD也相当于一根链杆2。于是,刚片CDE与基础之间用三根链杆1,2,3连接,这三根链杆的延长线交于一点O,故此体系为瞬变体系。

【例7.5】　试对如图7.21(a)所示体系进行几何组成分析。

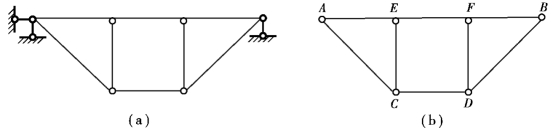
图7.21

【解】　因该体系用三根不全交于一点也不全平行的支座链杆与基础相连,故可直接取内部体系图7.21(b)进行几何组成分析。将AB视为刚片,再在其上增加二元体ACE和BDF,组成几何不变体系,链杆CD是添加在几何不变体系上的约束,故此体系为具有一个多余约束的几何不变体系。

【例7.6】　试对如图7.22所示体系进行几何组成分析。

【解】　杆AB的A处是固定端支座,故杆AB和基础组成几何不变体系,在B处的支座链杆是多余约束。因此,体系是几何不变的,且有一个多余约束。

【例7.7】　试对如图7.23所示体系进行几何组成分析。

【解】　将杆AB和基础分别视为刚片Ⅰ和刚片Ⅱ,刚片Ⅰ和刚片Ⅱ用固定铰支座A和链杆①相连,组成一个几何不变体系。现又在此体系上添加了三根链杆②、③、④,故整个体系为几何不变的,且有三个多余约束。

图7.22

图7.23