轴向拉压杆的强度计算

根据强度条件,可以解决工程中三种不同类型的强度计算问题:

①强度校核。已知杆的材料、尺寸和承受的荷载(即已知[σ],A和FNmax),要求校核杆的强度是否足够。此时只要检查式(5.22)是否成立。

②设计截面尺寸。已知杆的材料、承受的荷载(即已知[σ],FNmax),要求确定横截面面积或尺寸。为此,将式(5.22)改写为

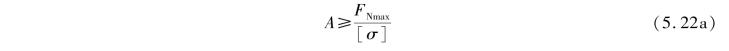
据此可算出必需的横截面面积。根据已知的横截面形状,再确定横截面尺寸。

工程中的杆件截面尺寸往往需要符合一定的模数,可能会遇到为了满足强度条件而需选用过大截面的情况。为经济起见,此时可以考虑选用小一号的截面,但由此而引起的杆的最大正应力超过许用应力的百分数应限制在5%以内,即

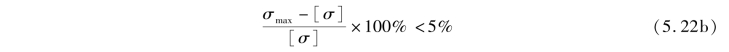
③确定许用荷载。已知杆的材料和尺寸(即已知[σ]和A),要求确定杆所能承受的最大荷载。为此,将式(5.22)改写为

先计算出杆所能承受的最大轴力,再由荷载与轴力的关系计算出杆所能承受的最大荷载。

特别指出:利用强度条件对受压直杆进行计算,仅对较粗短的直杆适用;而对于细长的受压杆件,承载能力主要取决于它的稳定性,稳定计算将在本书第12章讨论。

【例5.8】　如图5.29(a)所示三铰屋架的拉杆采用16锰圆钢,直径d=20mm。已知材料的许用应力[σ]=200MPa,试校核钢拉杆的强度。

图5.29

【解】　三铰屋架的计算简图如图5.29(b)所示。

①求支座反力。取整个屋架为研究对象〔图5.29(b)〕,利用对称性,得

②求拉杆的轴力。取半个屋架为研究对象〔图5.29(c)〕,由平衡方程

得

③求拉杆的最大正应力。钢拉杆是等直杆,横截面上的轴力相同,故杆的最大正应力为

④校核拉杆的强度。因为

σmax=182MPa<[σ]=200MPa

因此钢拉杆的强度是足够的。

【例5.9】　如图5.30(a)所示钢桁架的所有各杆都是由两个等边角钢组成。已知角钢的材料为Q235钢,其许用应力[σ]=170MPa,试为杆EH选择所需角钢的型号。

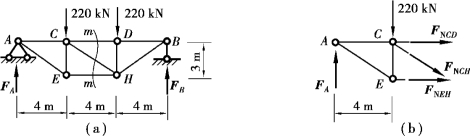
图5.30

【解】　①求支座反力。取整个桁架为研究对象〔图5.30(a)〕,由对称性得

FA=FB=F=220kN

②求杆EH的轴力。假想用截面m—m将桁架截开,取左边部分为研究对象〔图5.30(b)〕,由平衡方程

得

③计算杆EH的横截面积。由式(5.22)得(www.xing528.com)

④选择等边角钢的型号。型钢是工程中常用的标准截面(见附录Ⅱ)。等边角钢是型钢的一种。它的型号用边长的厘米数表示,在设计图上则常用边长和厚度的毫米数来表示,例如符号└80×7表示8号角钢,其边长为80mm,厚度为7mm。现由型钢表查得,厚度为6mm的7.5号等边角钢的横截面面积为8.797×102 mm2=879.7mm2,用两个这样的等边角钢组成的杆的横截面面积为879.7mm2×2=1759.4mm2,稍大于1720mm2。因此,选用└75×6。

【例5.10】　如图5.31(a)所示为正方形截面阶梯形柱。已知:材料的许用压应力[σc]=1.05MPa,弹性模量E=3GPa,荷载FP=60kN,柱自重不计。试校核该柱的强度。

图5.31

【解】　①画轴力图〔图5.28(b)〕。

②求AB段及BC段的应力。

③校核强度。

因此该柱满足强度要求。

【例5.11】　如图5.32所示的实心圆截面木杆,杆的直径沿轴线变化,A截面直径为dA=140mm,C截面直径为dC=160mm,B截面为AC杆的中点截面,木材的许用拉应力[σt]=6.5MPa,许用压应力[σc]=10MPa。求该杆的许用荷载[FP]。

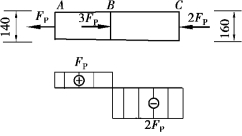
图5.32

【解】　①画出杆的轴力图,如图5.32所示。设外荷载FP的单位为kN,从轴力图可以看出:AB段受拉,A偏右截面为危险截面;BC段受压,B偏右截面为危险截面。各危险截面上的任一点均为危险点。

②利用强度条件确定各段的许用荷载。

[FNBC]=176.6kN

③确定许用的外荷载。从轴力图可得各段轴力与外荷载的关系为:

由AB段可得

由BC段可得

要使杆安全使用,那么就必须保证每一段都不破坏,所以许用荷载取上述计算结果的较小值,即[FP]=88.3kN。

【例5.12】　如图5.33(a)所示一等直杆,其顶部受轴向荷载F的作用。已知杆的长度为l,横截面面积为A,材料的容重为γ,许用应力为[σ],试写出考虑杆自重时的强度条件。

图5.33

【解】　杆的自重可看作沿轴线均匀分布的荷载〔图5.33(a)〕。应用截面法〔图5.33(b)〕,杆的任一横截面m—m上的轴力为

FN(x)=-(F+γAx)

负号表示轴力为压力。由此绘出杆的轴力图,如图5.33(c)所示。根部横截面上的轴力最大,其值为

FNmax=F+γAl(压)

由式(5.22)可得杆的强度条件为

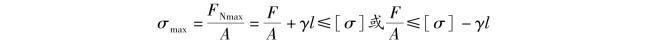
由此例可知,当考虑杆的自重时,相当于材料的许用应力减小了γl。若,则自重对杆的影响很小,可以忽略;若有一定数量的值,则自重对强度的影响应加以考虑。例如,有一长l=10m的等直钢杆,钢的容重γ=76440N/m3,许用应力[σ]=170MPa,则≪1;若有同样长度的砖柱,砖的容重γ=17640N/m3,许用应力[σ]=1.2 MPa,而。一般地,金属材料制成的拉压杆在强度计算中可以不考虑自重的影响(有些很长的杆件,如起重机的吊缆、钻探机的钻杆等除外);但对砖、石、混凝土制成的柱(压杆)在强度计算中应该考虑自重的影响。