建筑力学中的变形和应变特点

轴向拉伸与压缩杆主要产生沿杆轴线方向的伸长或缩短变形,这种变形称为纵向变形。同时,与杆轴线相垂直的方向(横向)也会随之产生缩小或增大的变形,通常称为横向变形。

本节将讨论轴向拉伸与压缩杆的变形计算。

(1)纵向、横向变形

如图5.12所示,设杆件原长为l,变形后的长度为l1,则杆件的纵向变形为

Δl=l1-l

其在轴向拉伸时为正,轴向压缩时为负,单位与杆件长度单位相同,常用m或mm。

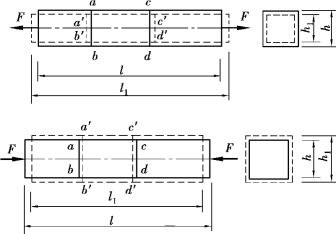
图5.12

杆的横向变形量为

Δh=h1-h

其在轴向拉伸时为负,轴向压缩时为正。

杆件的纵向变形量Δl或横向变形量Δh,只能表示杆件在纵向或横向的总变形量,不能说明杆件的变形程度。通常,对于长为l的杆段,若纵向变形为Δl,则用平均单位长度的纵向变形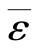来描述杆件的纵向变形程度。即

ε称为杆件的平均线应变,这里,“线”表示变形是长度变化,以区别于角度的变化。一般平均线应变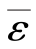是杆件长度l的函数。当l→0时(杆段成为一点),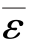所取极限值,称为该点的线应变,用ε表示。即

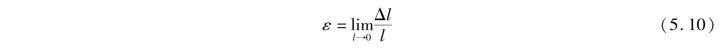(www.xing528.com)

对于轴力为常数的等直杆段,各横截面处纵向变形程度相同,则平均线应变与各点的线应变相同。因此,对这种杆段不再区别平均线应变与各点的线应变。本书主要讨论此种情形,以后不再说明。

ε称为纵向线应变,简称线应变。ε的正负号与Δl相同,拉伸时为正值,压缩时为负值。线应变ε是一个无量纲的量,常用小数、百分数或千分数来表示。

同理,单位长度的横向变形为

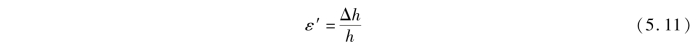
ε′称为横向线应变。ε′的正负号与Δh相同,压缩时为正值,拉伸时为负值,即横向线应变与纵向线应变恒异号;ε′也是一个无量纲的量。

(2)泊松比

大量的实验表明,当轴向拉(压)杆的应力不超过材料的比例极限时,横向线应变ε′与纵向线应变ε的比值的绝对值是一个常数。通常将这一常数称为泊松比或横向变形系数,用μ表示。即

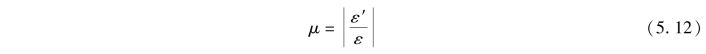
μ是一个量纲为1的量,其数值随材料而异,可通过试验进行测定。一些常用材料的μ的约值见表5.1。弹性模量E和泊松比μ是材料固有的两个弹性常数,以后将会经常用到。

表5.1　常用材料的E和μ的约值

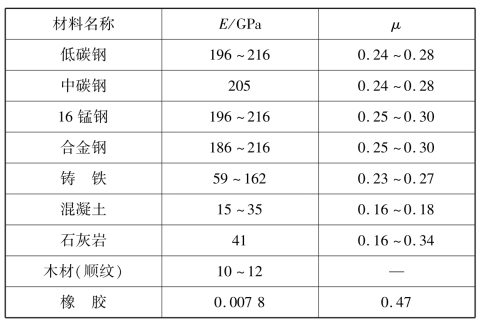
考虑到ε′与ε的正负号恒相反,由式(5.12)可得

利用上式,可由纵向线应变和泊松比求横向线应变;反之亦然。