轴向拉伸与压缩杆应力分布

要确定拉伸与压缩杆横截面上的应力,首先必须知道横截面上内力的分布规律。而横截面上内力的分布规律与变形有关。因此,先通过实验来观察杆件变形的情况。

用容易发生变形的橡胶棒制作一根等截面直杆,并在其表面均匀地画上一些与杆轴平行的纵线和与之垂直的横线,如图5.8(a)所示。在杆上施加轴向拉力,可以看到:所有纵线都伸长了,且伸长量相等;所有横线仍保持与杆轴线垂直,但每两相邻横线间的距离增大了,如图5.8(b)所示。

图5.8

据此现象,如果把该等直杆设想为由无数纵向纤维组成,各纤维之间无黏结,即每根纤维可自由伸缩。这是一种常用的等直杆力学模型,可以用这个模型解释观察到的等直杆轴向拉伸变形现象。依据实验现象,我们可以提出如下假设:等直杆在轴向拉力作用下,所有纵向纤维都伸长了相同的量;所有横截面仍保持为平面且与杆轴垂直(此即所谓的平截面假设),只不过相对离开了一定的距离。由此可以认为:轴向受拉杆件横截面上任一点都受到且只受到平行于杆轴方向(即与杆横截面垂直)的拉力作用,各点拉力大小相等。即杆横截面实际上是受到连续均匀分布的正向拉力作用,这些分布拉力的合力就是轴力,如图5.8(c)所示。

根据平面假设可知,内力在横截面上是均匀分布的。若杆轴力为FN,横截面面积为A,则单位面积上的内力为

式中,σ的方向与横截面正互,故称为横截面上的正应力,其符号与轴力的符号相对应,即拉应力为正,压应力为负。

【例5.4】　试求如图5.9所示杆件各段横截面上的应力。已知AB段和CD段的横截面面积为200mm2,BC段的横截面面积为100mm2,F=10kN。

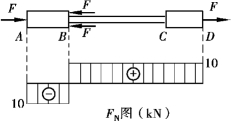
图5.9

【解】　①计算各段轴力,画轴力图。由截面法求得各杆段的轴力为

AB段:FN1=F=-10kN(压力)

BC段:FN2=F=10kN

CD段:FN3=F=10kN

②计算各段横截面上的应力。运用公式求得:

(www.xing528.com)

结果表明,该杆的最大应力发生在BC段。

【例5.5】　某轴向受力柱如图5.10(a)所示,柱顶受压力F,柱子所用材料的重度为γ。柱横截面为正方形,边长为a,柱高为H。求该柱内的最大应力。

图5.10

【解】　①求轴力函数,画轴力图。

在离顶端为x处截开,取杆件x段研究对象,此截面上的轴力为FN(x),该截面轴力为x的函数。受力情况如图5.10(b)所示。

由平衡方程

得

据此轴力函数作轴力图,如图5.10(c)所示。

由轴力图可以看出底面的轴力最大,等截面全柱受压的情况下,该截面为危险截面。最大轴力为FNmax=-F-γHa2。

②计算危险截面的最大正应力。

轴心受压情况下,正应力在横截面上均匀分布,故柱底截面上所有点应力大小一致,均为危险点,最大工作正应力为

注意:代入数据计算过程中,应考虑单位的换算,工程上应力的单位常用MPa。