静定物体系统的平衡问题解决方法

前面研究了平面力系单个物体的平衡问题,但是在工程结构中往往是由若干个物体通过一定的约束来组成一个系统,这种系统称为物体系统。例如,如图4.24(a)所示的组合梁,就是由梁AC和梁CD通过铰C连接,并支承在A,B,D支座而组成的一个物体系统。

在一个物体系统中,一个物体的受力与其他物体是紧密相关的,整体受力又与局部受力紧密相关。物体系统的平衡是指组成系统的每一个物体及系统的整体都处于平衡状态。

图4.24

在研究物体系统的平衡问题时,不仅要知道外界物体对这个系统的作用力,同时还应分析系统内部物体之间的相互作用力。通常将系统以外的物体对这个系统的作用力称为外力,系统内各物体之间的相互作用力称为内力。例如图4.24(b)所示的组合梁的受力图,荷载及A,B,D支座的反力就是外力,而在铰链C处左右两段梁之间互相作用的力就是内力。应当注意,外力和内力是相对的概念,是对一定的考察对象而言的,例如图4.24所示组合梁在铰链C处两段梁的相互作用力,对组合梁的整体来说,就是内力,而对左段梁或右段梁来说,就成为外力了。

当物体系统平衡时,组成该系统的每个物体都处于平衡状态,因而,对于每一个物体一般可写出3个独立的平衡方程。如果该物体系统有n个物体,而每个物体又都在平面一般力系作用下,则就有3n个独立的平衡方程,可以求出3n个未知量。但是,如果系统中的物体受平面汇互力系或平面平行力系的作用,则独立的平衡方程将相应减少,而所能求的未知量数目也相应减少。若用平衡方程能求出物体系统的全部约束力,则该物体系统称为静定的物体系统。

在求解静定物体系统的平衡问题时,可以选取整个物体系统作为研究对象,也可以选取物体系统中某个部分(一个物体或几个物体的组合)作为研究对象,以建立平衡方程求解未知量。通常可先选取整个系统为研究对象,看能否从中解出一个或几个未知量,然后再选取物体系统中某些部分为研究对象,求出其余未知量。解题的关键是恰当地选取研究对象,用最少的方程,并尽量使一个方程中只包含一个未知量,以简化计算。

下面举例说明求解静定物体系统平衡问题的方法。

【例4.12】　组合梁AC及CE用铰链C连接而成,受力情况如图4.25(a)所示。设F=50kN,q=25kN/m,M=50kN·m。求各支座反力。

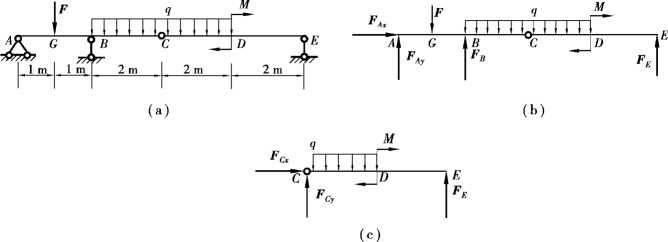
图4.25

【解】　先以整体为研究对象,组合梁在主动力F,q,M和约束力FAx,FAy,FB及FE的作用下平衡,如图4.25(b)所示。列平衡方程

以上3个方程中包含有4个未知量,必须再补充方程才能求解。为此可取梁CE为研究对象,受力如图4.25(c)所示。列力矩方程

由式(d)得

FE=25kN

将求得的FE代入(a),(b),(c)式得(www.xing528.com)

FAx=0　FAy=-25kN　FB=150kN

FAy的结果为负,说明其实际方向与假设方向相反。

【例4.13】　三铰刚架荷载如图4.26所示,其中F1=30kN,F2=20kN,求A,B处支座反力。

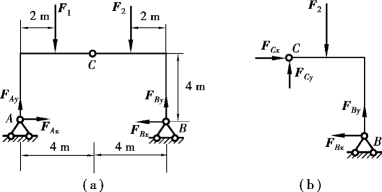
图4.26

【解】　①先取整体为研究对象,注意在研究整体时,铰链C传递的力属于内力,故在受力图和平衡方程中不出现。受力图如图4.26(a)所示。

②列平衡方程

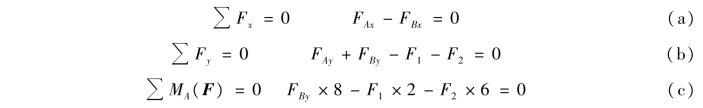
由方程(b)和(c),得

FBy=22.5kN　　FAy=27.5kN

③取CB为研究对象。对CB来讲,铰链C处传递的力属于外力,要考虑。受力图如图4.26(b)所示。列平衡方程,得

可求得

FBx=12.5kN

将FBx=12.5kN代入(a)式,得

FAx=12.5kN