建筑力学（第2版）：平面力系的平衡方程

平面力系向平面内任一点简化后,若主矢和主矩同时为零,则力系平衡;反之,若力系平衡,则主矢和主矩必然都等于零。因此,平面一般力系平衡的充分必要条件是:力系的主矢和对任一点的主矩都为零。其解析条件可表示为

即

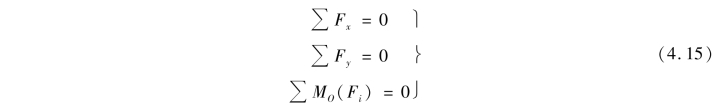
方程组(4.15)是平面一般力系的平衡方程,称为一矩式方程组。其中,前两式称为投影方程,第三式称为力矩方程,这组方程是平面一般力系平衡的基本形式。它表明平面一般力系平衡的充分必要条件是:力系中各力在两个直角坐标轴上的投影的代数和等于零,且各力对任一点之矩的代数和也等于零。平面力系的平衡方程除了式(4.15)所示的基本形式外,还有二矩式和三矩式方程。

二矩式方程:

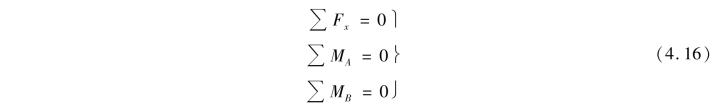
式中,x轴不能与A,B两点的连线垂直。

为何这组方程也能表示力系的平衡呢?这是因为当力矩方程成立时,力系便不可能简化成为力偶,只可能简化为一个合力或处于平衡。若简化为合力,其作用线必通过矩心A,B两点的连线,如图4.19所示。方程中要求A,B两点连线不能垂直于x轴,且,那么只有合力为零时,才能满足这个条件。

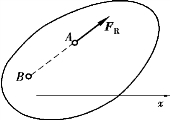
图4.19

三矩式方程:

若两个投影方程全部用力矩方程代替,则有

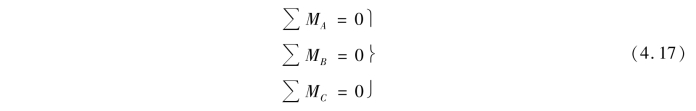
式中,A,B,C三点不共线。

为何这组方程也能表示力系的平衡条件呢?由上述三个方程可知,力系不可能简化成为力偶。若力系简化为合力,则合力要过A,B,C三点,但由于此三点不共线,故力系不可能有合力,只能保持平衡。

上述三组方程(4.15)、(4.16)、(4.17)应选哪一组方程求解,要根据具体条件确定。

【例4.9】　外伸梁AD,A端为固定铰支座,B处为滑动铰支座。梁长6m,C处作用集中荷载80kN,BD段作用均布荷载5kN/m,如图4.20(a)所示。求A,B两处支座反力。

【解】　①取AD梁为研究对象。它所受的主动力有:集中荷载80kN,均布荷载5kN/m。它所受的约束力有:固定铰支座A处的两个分力FAx和FAy,滑动铰支座B处的FB。梁AD的受力图如图4.20(b)所示。

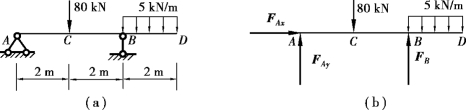(https://www.xing528.com)

图4.20

②列平衡方程:

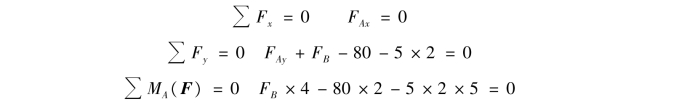
解上述方程,得

FAy与FB的值均为正,说明其实际方向与假设方向相同。

【例4.10】　在如图4.21(a)所示的刚架中,已知q=3kN/m,F=6kN,M=10kN·m,不计刚架自重。求固定端A处的约束力。

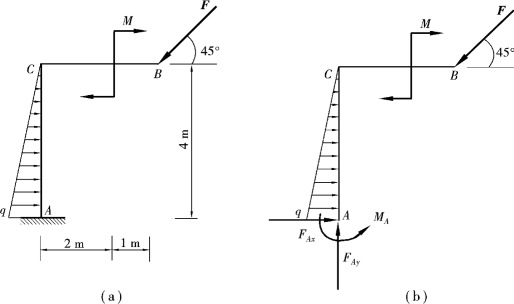
图4.21

【解】　①取刚架为研究对象。其上除受主动力外,还受有固定端A处的约束力FAx,FAy和约束力偶MA,如图4.21(b)所示。

②列平衡方程:

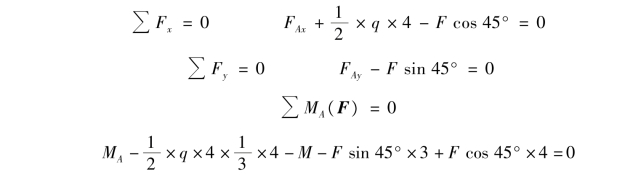
解得:

FAy与MA均为正,说明其实际方向与假设方向相同。

从上述例题可见,选取适当的坐标轴和力矩中心,可以减少每个平衡方程中的未知量的数目。在平面一般力系情形下,矩心应尽量取在多个未知力的互点上,而坐标轴应当与尽可能多的未知力相垂直。

在例4.9中,若以方程取代方程,可以不解联立方程直接求得FAy的值。因此在计算某些问题时,采用力矩方程往往比投影方程简便。

对于受平面一般力系作用的单个刚体的平衡问题,只能列出三个独立的平衡方程,求解三个未知量。对于另外写出的投影方程或力矩方程,只能用来校核计算结果。