简化结果的讨论-建筑力学

平面一般力系向作用平面内任一点简化,一般可得到一个主矢和一个主矩MO,根据主矢和主矩是否为零,可分为以下4种情况:

①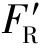=0,MO≠0。此时,原力系简化为一个合力偶,合力偶矩等于主矩。因为力偶对于平面内任意一点的矩都相同,所以当力系合成为一个力偶时,主矩与简化中心的位置无关。

②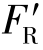≠0,MO=0。此时,原力系简化为一个合力,合力的大小、方向与主矢相同,合力的作用线通过简化中心。

③≠0,MO≠0。此时,原力系仍可简化为一个合力。现将矩为MO的力偶用两个等值、反向的平行力FR和来替换,且=FR=-,如图4.17(a)、(b)所示。于是,与为一对平衡力,根据加减平衡力系公理,可将这对平衡力消去,从而使原力系简化为一个作用线过O′点的合力FR〔图4.17(c)〕。合力FR的大小、方向与主矢相同,合力的作用线不通过简化中心。合力的作用线在O点的哪一侧,需根据主矢和主矩的方向确定。O点到合力作用线的距离d为

图4.17

由图4.17(c)可以看出,平面力系的合力FR对O点之矩为

MO(FR)=FRd

因为

故

由于简化中心O是任意选取的,故上式具有普遍意义。于是可得到平面一般力系的合力矩定理:平面一般力系的合力对其作用面内任一点之矩等于力系中各力对同一点之矩的代数和。利用该定理,可以简化某些情况下的力矩计算,还可以确定平面力系合力作用线的位置。

④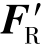=0,MO=0。此时,原力系处于平衡状态。

【例4.8】　长度为l的简支梁AB受三角形分布荷载作用,其分布荷载集度的最大值为q0,如图4.18所示。试求该分布力系合力的大小及作用线位置。(www.xing528.com)

图4.18

【解】　建立直角坐标系xAy,如图4.18所示。荷载集度是坐标x的函数,梁上距A端x处的荷载集度为

在该处长度为dx的微段上,荷载的大小为q(x)dx,因此整个梁上分布荷载的合力为

方向竖直向下。

再确定该分布荷载合力作用线的位置。设合力作用线距离A端的长度为a,在距A端x处长度为dx的微段上的力q(x)dx对A的力矩为q(x)dx·x,根据合力矩定理可得

将(a)、(b)两式代入(c)式得

解得

计算表明,三角形分布荷载,其合力的大小等于三角形分布荷载的面积,合力的作用线通过该三角形的几何中心。

同理,均布荷载,其合力的大小等于均布荷载的面积,合力的作用线通过该矩形的几何中心。请读者自行证明。