建筑力学：平面力系简化

设刚体受一平面一般力系F1,F2,…,Fn作用,如图4.16(a)所示。在力系的作用面内任选一点O,称为简化中心。应用力的平移定理,将各力平移至O点,同时附加相应的力偶,便可得到一个平面汇互力系,,…,和一个平面力偶系M1,M2,…,Mn,如图4.16(b)所示。根据力的平移定理可知:

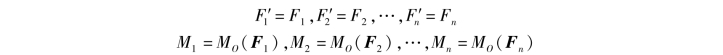
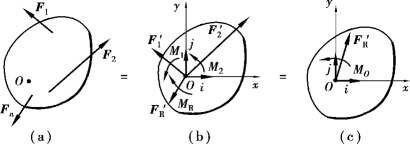
图4.16

平面汇互力系,,…,又可合成为作用于O点的一个合力,即

由于

因此

为原力系各力的矢量和,称为原平面力系的主矢。显然,主矢并不能代替原力系对物体的作用,因而它不是原力系的合力,它只代表力系中各力的矢量和,与简化中心无关。主矢的大小和方向为(www.xing528.com)

式中　,——主矢在x轴和y轴上的投影;

α——主矢与x轴正向之间的夹角。

附加的力偶系M1,M2,…,Mn可按平面力偶系合成的方法,将其合成为一个合力偶,合力偶矩为

MO=M1+M2+…+Mn

因各力平移时所附加的力偶矩分别为原力对简化中心O之矩,即

式中　MO——原力系对简化中心O点的主矩,等于原力系中各力对简化中心之矩的代数和。

显然,主矩不能代替原力系对物体的作用,即不是原力系的合力偶矩。

综上所述,可得以下结论:一般情况下,平面一般力系向平面内任一点简化,可得到一个力和一个力偶〔图4.16(c)〕。该力称为原力系的主矢,它等于力系中各力的矢量和,其大小和方向与简化中心无关,但作用线通过简化中心;该力偶的力偶矩称为原力系对简化中心的主矩,它等于原力系中各力对简化中心之矩的代数和,其值一般与简化中心有关。