平面汇交力系的解析条件

平面汇互力系平衡的充分和必要条件是:该力系的合力为零。即

欲使上式成立,必须同时满足

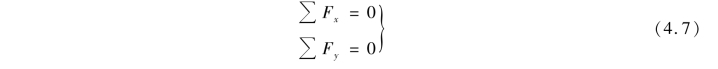
即平面汇互力系平衡的解析条件为各力在两个坐标轴上投影的代数和分别为零。式(4.7)称为平面汇互力系的平衡方程。

下面举例说明平面汇互力系平衡方程的应用。

【例4.4】　用解析法求解例题4.1。

【解】　①选取刚架为研究对象。

②画受力图。刚架在B处受荷载F的作用。D处为滑动铰支座,它对刚架D处的约束力FD的作用线垂直于支承面。A处为固定铰支座,约束力FA的作用线可根据三力平衡汇交定理确定,它通过另外两个力的作用线的汇交点C,如图4.9(b)所示。

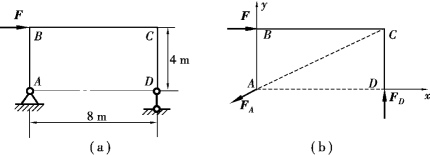
图4.9

③建立直角坐标系,如图4.9(b)所示,列平衡方程:

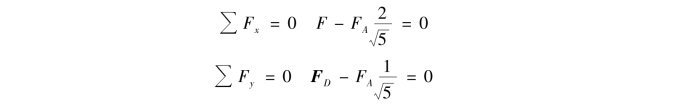
④解方程得:(www.xing528.com)

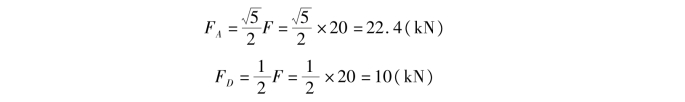
FA与FD的结果为正,说明FA和FD的实际方向与假设方向相同。

【例4.5】　如图4.10(a)所示,三角支架由杆AB,AC铰接而成,在铰A处作用着力F,F=10kN,杆的自重不计,试求出杆AB,AC所受的力。

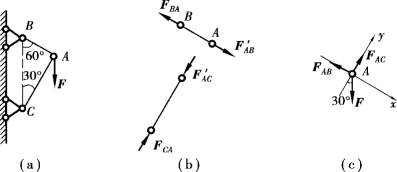
图4.10

【解】　①选取研究对象。AB,AC两杆都是二力杆,假设杆AB受拉力,杆AC受压力,受力图如图4.10(b)所示。需要指出的是,二力杆通常被看成一种约束,其受力图可以不画,因此可以省略图4.10(b)。为了求出这两个未知力,可求两杆对铰链A的约束力。因此,选取铰链A为研究对象。

②画受力图。铰链A受力F作用,此外受杆AB和AC的约束力作用,分别为FAB和FAC。这些力组成了平面汇交力系,如图4.10(c)所示。

③列平衡方程。选取坐标轴如图4.10(c)所示,坐标轴应尽量取在与未知力作用线垂直的方向。这样在一个平衡方程中只有一个未知量,不必联立求解方程组。即

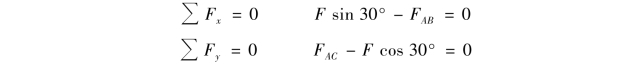
④解方程得:

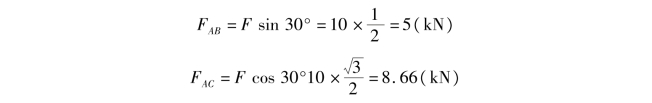
FAB和FAC为正值,说明力的假设方向与实际方向相同,即AB杆受拉,AC杆受压。