平面力系合成解析法及其应用

求解平面汇互力系问题,除了应用几何法外,经常应用的是解析法。解析法是以力在坐标轴上的投影为基础的。因此先介绍力在坐标轴上的投影的概念。

(1)力在坐标轴上的投影

如图4.4所示,设力F在直角坐标系xOy平面内,从力F的起点A和终点B分别向Ox轴作垂线,得到垂足a,b,线段ab称为力F在x轴上的投影,记作Fx。同理,从力F的起点A和终点B向Oy轴作垂线,得到垂足a′,b′,线段a′b′称为力F在y轴上的投影,记作Fy。

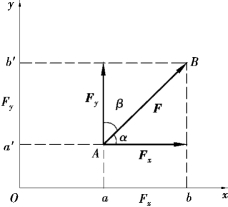
图4.4

力在坐标轴上的投影是代数量,其正负号的规定为:从起点A的投影a(或a′)到终点B的投影b(或b′)的指向与坐标轴的正向相同时,投影为正;反之为负。

设α和β分别表示力F与直角坐标系x和y轴正向间的夹角,则力F在x,y轴上的投影分别为

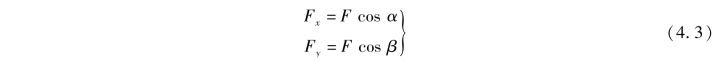
两种特殊情况:当力与轴垂直时,力在该轴上的投影为零;当力与轴平行时,力在该轴上投影的绝对值等于该力的大小。

反之,若已知力F在直角坐标系x,y轴上的投影Fx,Fy,由图4.4可求出该力的大小和方向,即

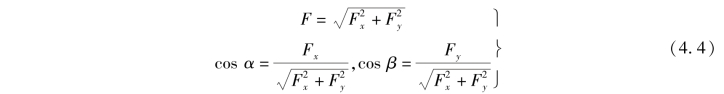
【例4.2】　试分别求出图4.5中各力在x轴和y轴上的投影。已知力F1,F2的大小均为200kN。

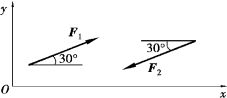
图4.5

【解】　F1x=F1cos30°=200×0.866=173.2(kN)

F1y=F1sin30°=200×0.5=100(kN)

F2x=-F2cos30°=-200×0.866=-173.2(kN)

F2y=-F2sin30°=-200×0.5=-100(kN)

(2)合力投影定理

设刚体受一平面汇互力系F1,F2和F3作用,此三力汇互于O点〔图4.6(a)〕,用力多边形法则可得其合力FR〔图4.6(b)〕。在力系作用平面内建立直角坐标系Oxy,将合力FR及各分力F1,F2和F3分别向x轴进行投影,得FRx=ad,F1x=ab,F2x=bc,F3x=-cd。由图4.6(b)可知:

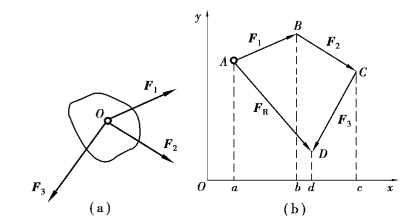
图4.6

ad=ab+bc-cd(www.xing528.com)

故

FRx=F1x+F2x+F3x

同理可得

FRy=F1y+F2y+F3y

将上述关系式推广至由n个力组成的平面汇互力系,可得

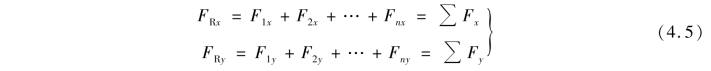
式(4.5)称为合力投影定理。它表明平面汇互力系的合力在某轴上的投影等于力系中各分力在同一轴上投影的代数和。

(3)平面汇互力系合成的解析法

根据合力投影定理,求出合力FR的投影FRx及FRy后(图4.7),即可按式(4.4)求出合力FR的大小及方向。

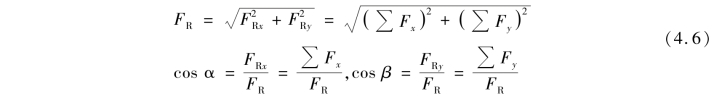
【例4.3】　如图4.8所示平面汇交力系,已知F1=3kN,F2=1kN,F3=1.5kN,F4=2 kN。试求此力系的合力FR。

【解】　建立直角坐标系Oxy(图4.8),合力在坐标轴上的投影分别为:

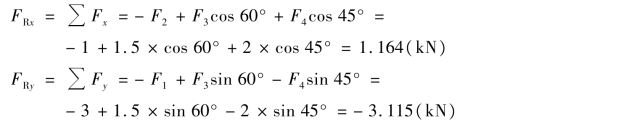
由式(4.6),合力FR的大小为

合力FR与x轴间所夹锐角α为

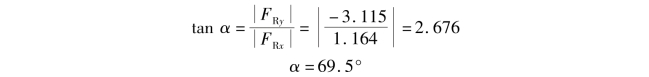
由FRx与FRy的正负号可判断合力FR应指向右下方,如图4.8所示。

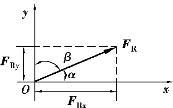
图4.7

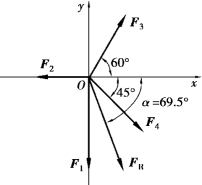
图4.8