建筑力学第2版：平面汇交力系合成的几何法

第2章已经介绍了用平行四边形法则或三角形法则求两个汇互于一点的力的合力,这种方法称为几何法。当求更多的汇互于一点的力的合力时,也可以用几何法,下面举例说明。

刚体受一平面汇互力系F1,F2,F3和F4作用,力的大小及方向如图4.2(a)所示,现求该力系的合力。为此,可连续使用力的三角形法则,即先求F1与F2的合力FR1,再求FR1与F3的合力FR2,最后求FR2与F4的合力FR,FR便是此平面汇互力系的合力,如图4.2(b)所示。

由图4.2(b)可见,在作图过程中,力FR1,FR2可不必画出。更简便的合成方法是:各分力矢首尾相接,则画出一条矢量折线A—B—C—D—E,如图4.2(c)所示,然后从第一个力矢F1的起点A向最后一个力矢F4的终点E作一个矢量,以使折线封闭而成为一个多边形,则由A点指向E点的封闭边AE就代表了该力系的合力矢FR的大小和方向,合力的作用线通过原力系的汇互点。该多边形称为已知力系的力多边形。这种求合力的方法称为力多边形法则。

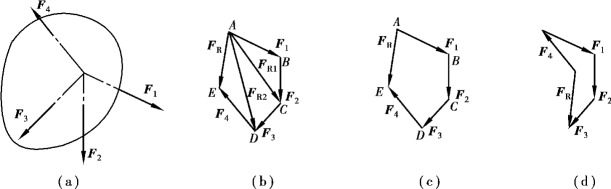
图4.2

在利用力多边形法则求平面汇互力系的合力时,根据矢量相加的互换律,任意变换各分力矢的作图次序,可得到形状不同的力多边形,但其合力矢仍然不变,如图4.2(d)所示。(www.xing528.com)

综上所述,可得如下结论:平面汇互力系合成的结果是一个合力,其大小和方向由力多边形的封闭边来表示,其作用线通过各力的汇互点,即合力等于各分力的矢量和。设平面汇互力系包含n个力,以FR表示它们的合力矢,则有

一般可以略去求和符号中的&=1,n。这样上式可以简写为

注意:力多边形的封闭边仅表示合力的大小和方向,合力的作用线通过力系的汇交点。另外,合成结果与各力的绘制顺序无关。