绘制单代号网络图的方法及步骤

单代号网络计划是以节点及其编号表示工作，以箭线表示工作之间逻辑关系的网络计划。在单代号网络图的节点中标注工作编号、工作名称和工作持续时间，以形成单代号网络计划，如图5.62所示。

图5.62　单代号网络计划图

1）单代号网络计划的特点

单代号网络计划与双代号网络计划相比，具有以下特点：

①工作之间的逻辑关系容易表达，且不用虚箭线，故绘图较简单。

②网络图便于检查和修改。

③由于工作持续时间表示在节点之中，没有长度，故不够直观。

④表示工作之间逻辑关系的箭线可能产生较多的纵横交叉现象。

2）单代号网络图的基本符号

（1）节点

单代号网络图中的每一个节点表示一项工作，节点宜用圆圈或矩形表示。节点所表示的工作名称、持续时间和工作编号等应标注在节点内，如图5.63所示。

单代号网络图中的节点必须编号，编号标注在节点内，其号码可间断，但严禁重复。箭线的箭尾节点编号应小于箭头节点编号，一项工作必须有唯一的一个节点及相应的一个编号。

图5.63　单代号网络图工作的表示方法

（2）箭线

在单代号网络图中，箭线表示工作之间的逻辑关系，它既不占用时间，也不消耗资源。箭线应画成水平直线、折线或斜线。箭线水平投影的方向应自左向右，表示工作的行进方向。工作之间的逻辑关系包括工艺关系和组织关系，在网络图中均表现为工作之间的先后顺序。

（3）线路

单代号网络图中，各条线路应用该线路上的节点编号从小到大依次表述。

3）单代号网络图的绘图规则

①单代号网络图必须正确表达已确定工作间的逻辑关系。

②单代号网络图中，不允许出现循环回路。

③单代号网络图中，不能出现双向箭头或无箭头的连线。

④单代号网络图中，不能出现没有箭尾节点的箭线和没有箭头节点的箭线。

⑤绘制单代号网络图时，箭线不宜交叉，当交叉不可避免时，可采用“暗桥”或“断线”的方法绘制，同双代号网络图的绘制。

⑥单代号网络图中，只有一个起始节点和一个终点节点。当网络图中有多个起始节点或多个终点节点时，应在网络图的前端或后端设置一项虚工作（节点），作为该网络图的起始节点（St）或终点节点（Fin）。

单代号网络图的绘图规则基本与双代号网络图的绘图规则相同，故不再进行解释。

4）单代号网络图的绘制

（1）单代号网络图的绘制模型（与双代号相比较）

虽然单代号网络图与双代号网络图在绘图的符号所表示的意义上不同，但所表达的计划内容是一致的。单代号网络图的绘制过程与双代号网络图的绘制过程一样，也是先进行项目结构分解，然后确定具体工作间的逻辑关系以及各项工作的持续时间。

①两项工作同时开始、同时结束（图5.64）。

图5.64　两项工作同时开始、同时结束

②约束关系。

a.全约束（图5.65）。

图5.65　全约束

b.半约束（图5.66）。

图5.66　半约束

c.三分之一约束（图5.67）。

图5.67　三分之一约束

（2）单代号网络图的绘制

绘制如表5.48所示工作逻辑关系的单代号网络图。

表5.48　工作逻辑关系表

单代号网络图如图5.68所示。

图5.68　单代号网络图

总结：

①单代号网络图的绘制比较简单，其各项工作之间的逻辑关系容易表达。

②单代号网络图的绘制不用虚箭线，便于检查和修改。

③需要常用“暗桥法”或“断线法”，解决交叉问题。

④因为单代号网络图无节点时间参数，所以不能改画成时标网络图。

【任务30】 已知工作之间的逻辑关系如表5.49所示，绘制单代号网络图。

表5.49　工作逻辑关系表

5）单代号网络计划时间参数的计算

单代号网络计划时间参数的计算应在确定各项工作的持续时间之后进行。时间参数的计算顺序和计算方法基本上与双代号网络计划时间参数的计算相同。单代号网络计划时间参数的标注如图5.69所示。

图5.69　单代号网络计划时间参数的标注

单代号网络计划时间参数的计算步骤如下：

（1）计算工作最早开始时间和最早完成时间

①工作最早开始时间ES。工作的最早开始时间表示该工作的所有紧前工作都已完成，本工作可以开工。

计算方法：从开始节点开始，顺着箭线的方向依次计算每一个节点，只看内向箭线，取所有紧前工作中最早完成时间的最大值，作为该工作最早开始时间ES，直至结束节点。

规定：开始节点最早开始时间为零，即ES1=0。

其中，h工作为i工作的紧前工作。

②工作最早完成时间EF。工作的最早完成时间EFi为：(www.xing528.com)

式中 ti——i工作的持续时间。

（2）网络计划的计算工期Tc

计算工期Tc等于网络计划的终点节点n的最早完成时间EFn，即：

（3）计算相邻两项工作之间的时间间隔LAGi，j

相邻两项工作i和j之间的时间间隔LAGi，j等于紧后工作j的最早开始时间ESj和本工作i的最早完成时间EFi之差，即：

（4）计算工作时差

①工作总时差TF。工作的总时差TFi应从网络计划的终点节点开始，逆着箭线的方向依次逐项计算。网络计划终点节点的总时差TFn，如计划工期Tp等于计算工期Tc，其值为零，即：

其他工作的总时差TFi等于该工作的各个紧后工作的总时差TFj加该工作与其紧后工作之间的时间间隔LAGi，j之和的最小值，即：

②工作自由时差FF。网络计划终点节点的自由时差FFn等于计划工期Tp减该工作的最早完成时间EFn，即：

其他工作的自由时差FFi等于该工作与其紧后工作j之间的时间间隔LAGi，j的最小值，即：

（5）计算工作的最迟开始时间和最迟完成时间

①工作的最迟完成时间LF。工作的最迟完成时间LFi应从网络计划的终点节点开始，逆着箭线的方向依次逐项计算。当部分工作分期完成时，相关工作的最迟完成时间应从分期完成的节点开始逆着箭线的方向依次逐项计算。

工作的最迟完成时间应按下列步骤进行：

终点节点（工作）n的最迟完成时间LFn，应按网络计划的计划工期Tp确定，即：

其他节点（工作）i的最迟完成时间LFi应为：

②工作的最迟开始时间LS。工作的最迟开始时间LSi表示该工作开工不能迟于这个时间，若迟于这个时间，将会影响网络计划的计划工期Tp。

工作的最迟开始时间LSi应按下式计算：

或

（6）关键工作及关键线路的确定

①关键工作的确定。单代号网络计划中，总时差最小的工作是关键工作。当计划工期Tp等于计算工期Tc时，关键工作的总时差为零，也是最小的总时差。当有要求工期Tr，且要求工期Tr小于计算工期Tc时，总时差最小值为负值；当要求工期大于计算工期时，总时差最小值为正值。

②关键线路的确定。在单代号网络计划中，从起始节点开始到终点节点均为关键工作，且所有工作的时间间隔均为零（即LAGi，j=0）的线路应为关键线路；或者线路上各项工作持续时间之和最长的是关键线路。关键线路在单代号网络计划中应用粗线或双线标注。

【案例5.29】 已知工作之间的逻辑关系如表5.50所示，绘制单代号网络计划图。若计划工期等于计算工期，试计算各项工作的6个时间参数并确定关键线路，标注在网络计划图上。

表5.50　工作逻辑关系表

【解】 绘制单代号网络计划图如图5.70所示。

图5.70　单代号网络计划图

各项工作的6个时间参数图上算法及关键线路如图5.71所示。

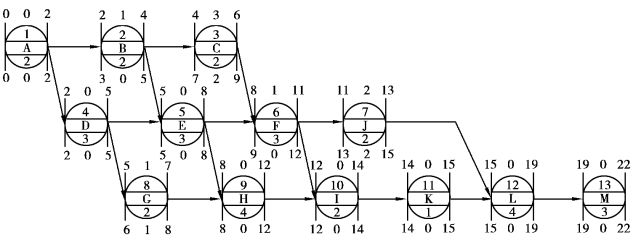
图5.71　单代号网络计划时间参数计算总图

（1）计算工作最早开始时间和最早结束时间

规定开始节点最早开始时间为零，即：

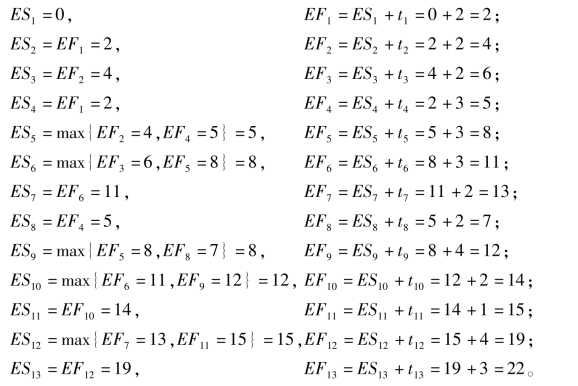
（2）网络计划的计算工期Tc

计算工期Tc等于网络计划的终点节点13的最早完成时间EF13，即：

Tc=EF13=22

（3）计算相邻两项工作之间的时间间隔LAGi，j

（4）工作时差的计算

①工作总时差TF。网络计划终点节点的总时差TF13，在假设计划工期Tp等于计算工期Tc时，其值为零，即：

TF13=0

其他工作的总时差TFi=min（TFj+LAGi，j）（j是i的紧后工作），即：

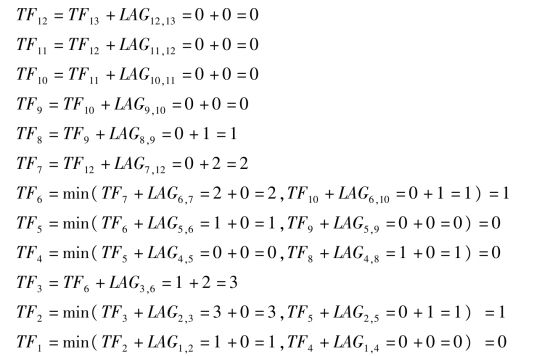
②工作自由时差FF。网络计划终点节点的自由时差FF13等于计划工期Tp减该工作的最早完成时间EF13，计划工期Tp等于计算工期Tc，即：

FF13=Tp-EF13=22-22=0

其他工作的自由时差FFi=min（LAGi，j）（j是i的紧后工作），即：

（5）工作最迟开始时间和最迟结束时间

终点节点（工作）13的最迟完成时间LF13=Tp=22。

工作最迟开始时间LSi=LFi-tj或LSi=ESi+TFi，即：

LS13=LF13-t13=22-3=19或LS13=ES13+TF13=19+0=19

其他节点（工作）i的最迟完成时间LFi=EFi+TFi，即：

（6）关键工作及关键线路的确定

总时差最小的工作是关键工作。当计划工期Tp等于计算工期Tc时，关键工作的总时差为零，也是最小的总时差。

在单代号网络计划图中，从起始节点开始到终点节点均为关键工作，且所有工作的时间间隔均为零（即LAGi，j=0）的线路应为关键线路。该单代号网络计划的关键线路为：A—D—E—H—I—K—L—M或①—④—⑤—⑨—⑩———，该线路上各项工作持续时间之和为22，是该网络计划图中持续时间最长的线路。关键线路在单代号网络计划中用粗线或双线标注。

【任务31】 同任务17，已知工作之间的逻辑关系及工作持续时间，绘制单代号网络计划图。若计划工期Tp等于计算工期Tc，计算各项工作的6个时间参数及LAGi，j，并确定关键线路。