提升双代号网络计划效率

网络计划的优化是指在编制阶段，在满足既定约束的条件下，按照一定目标通过不断改进网络计划方案，寻求满意结果，从而编制可供实施的网络计划的过程。

网络计划的优化目标包括工期、资源和费用。通过网络计划优化实现这些目标具有重大实际意义，甚至会使项目施工取得重大的经济效果。优化只是相对地获得近似的结果，不可能做到绝对优化。本节只重点介绍工期优化、工期-资源优化和工期-成本优化的基本原理及优化过程。

1）工期优化

当初步网络计划的计算工期大于合同要求或计划工期时，应通过压缩关键线路上关键工作的持续时间来满足工期的要求。

（1）工期优化的程序

①找出初步网络计划的关键线路及关键工作。

②按要求工期的要求计算应压缩的时间。

③确定各关键工作能压缩多少时间。

注意：该程序包含了3层含义：第一是哪些工作可以压缩，即压缩对象选择的问题；第二是压缩时采取的措施，即如何压缩的问题；第三是具体压缩多长时间的问题。

④调整关键工作的持续时间，并重新计算网络计划的计算工期。

⑤如果已经达到工期要求，则优化完成，否则重复以上程序，直至满足要求。

（2）压缩对象的选择

①选择那些压缩持续时间后对工程项目质量影响不大的关键工作。

②选择有充足备用资源的关键工作。

③选择能缩短工作持续时间且增加费用最少的工作。

注意：如果网络计划有多条关键线路，可考虑压缩共用的关键工作，或两条关键线路上的关键工作同时压缩同样的时间；每次压缩后要注意关键线路是否有变化（转移或增加条数）。

（3）压缩关键工作持续时间的措施

为使关键工作取得可压缩时间，必须采取一定的措施，这些措施主要有：增加资源数量、增加工作班次、组织流水作业、采取技术措施、改变施工方法等。若这些方法均不能满足要求，则只能改变工期要求或施工方案。

2）工期-资源优化

（1）工期规定，资源均衡

这种优化的前提是工期不变，使资源需要量尽量做到变化最小，接近于资源需要量的平均值，既有利于施工组织与管理，又可以取得好的经济效果。

劳动力等资源的消耗是否均衡，劳动力需求量图反映了施工期间劳动力的动态变化。它是衡量施工组织设计合理性的一个主要指标。不同的工程安排，劳动力需求量图呈现出不同的形状，一般可归纳为如图5.50所示的3种典型图示。图5.50（a）中出现短暂的劳动力高峰，图5.50（b）中劳动力需求量为锯齿波动形，这两种情况都不便于施工组织管理并增大了临时生活设施的规模，应尽量避免。图5.50（c）在一个较长的时间段内劳动力保持平衡，符合施工规律，是最理想的状况。

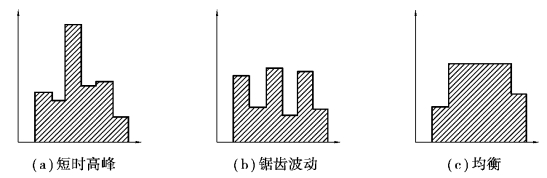
图5.50　劳动力需求量图

劳动力消耗的均衡性，用劳动力不均衡系数K表示，它应大于或等于1，越接近于1越合理，一般不允许超过1.5。其计算式为：

式中 Rmax——施工期间人数高峰值；

R平均——施工期间加权平均人数，即总劳动量/计划总工期。

在工期限定的条件下，当资源需求出现“高峰”时，通过对非关键工作进行调整，以使资源需求尽量达到均衡。调整的方法有以下两种：

第一，利用时差，推迟某些工作的开始时间。推迟规则为：优先推迟资源需要量小的工作；当有几项工作的资源需要量相同时，优先推迟富余时间大的工作。

第二，在条件允许的情况下，可在资源需要量超限的区段内中断某些工作，以减少对资源的需要量。

若以上方法均不能达到预期效果，可考虑改变某些工作的持续时间。

（2）资源有限，工期最短

为了简化问题，假定所有的工作都需要同一种资源。工期-资源优化的程序如下：

第1步，按节点最早开始时间绘制时标网络图及资源需求动态曲线。

第2步，从开始日期起，逐日检查每日资源需要量是否超过资源限量。如果所有时间段内均满足资源限量要求，则初步网络计划可行，否则要进行调整。

第3步，对资源有冲突区段的工作进行分析，看有哪些工作不能同时进行，需要将一项工作移到另一项工作之后进行，以降低资源需要量。假定在资源冲突区段内有i、j两项工作不能同时进行，把工作j移到工作i之后进行，如图5.51所示。

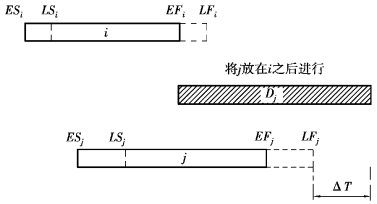
图5.51　i、j两项工作排序

则工期延长值为：

这样对资源有冲突区段的工作进行两两排序，得出若干个增加的ΔT，选择其中最小的（即延长工期最短的），将一项工作（j）移到另一项工作（i）之后进行。从式（5.22）中可以看出，是把资源需求高峰区段中值大的工作移到值小的工作之后进行。

注意：①若工作T LS的最大值和工作T EF的最小值属于同一项工作，就应找出工作T LS的次大值和工作T EF的次小值，次大值和最小值、最大值和次小值两两组合成两个方案，从中选择最佳方案（ΔT最小的）。

②若资源需求高峰区段有两项以上工作，依旧在所有工作中选择T LS的最大值和T EF的最小值作为移动的方案。

③若ΔT≤0，则说明工期不会延长。

第4步，每调整一次要重新绘制时标网络图，绘制资源需求动态曲线，再逐日检查，发现有资源冲突时再进行调整，如此循环，直至资源需要量满足资源供应限量，便可得到可行方案。

如果不调整资源需求计划，则应增加资源供应，会造成直接费用增加；而经过调整后工期延长，还会使间接费增加。所以，在调整的过程中要进行全方位考虑比较，如果因工期延长而增加的间接费大于因增加资源供给而增加的直接费，那就不应当调整，否则应通过调整找到最佳方案。

【案例5.27】 图5.52为某公路施工项目网络计划图。箭线下的数字是工作持续时间，箭线上的数字是工作资源强度。假定施工期间每天可供资源为10，试寻找新的工期安排。

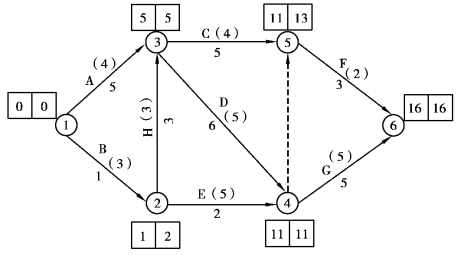
图5.52　某公路施工项目网络计划图

优化步骤如下：

第1步，绘制时标网络计划图（如图5.53上方所示）及资源需要量曲线（如图5.53下方所示）。

第2步，逐日检查资源是否满足要求。第2 d、第3 d资源需要量超过了限量，即12＞10，故要调整。这一区段共有3项工作：①—③、②—③、②—④。这3项工作的最早完成时间与最迟开始时间如表5.41所示。

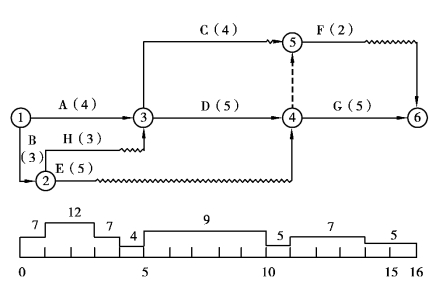
图5.53　绘制时标网络及资源需要量曲线

表5.41　3项工作时间表（1）

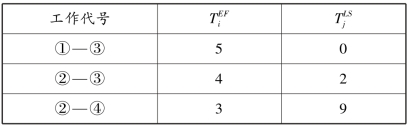
第3步，对资源冲突区段的工作进行分析。由表5.41中时间参数判断，的最大值和的最小值属于同一项工作②—④，所以分别找的次大值和的次小值所对应的工作是②—③工作。因为=3-2=1大于=4-9=-5（小于0说明工期不延长），所以将②—④工作移动到②—③工作之后进行。移动后的时标网络计划图及资源需要量曲线如图5.54所示。

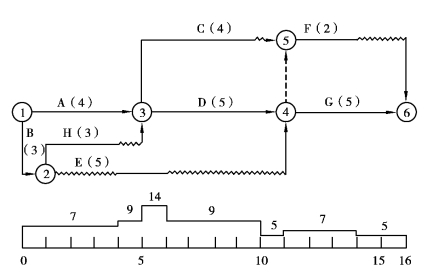
图5.54　一次移动后的时标网络及资源需要量曲线

第4步，再逐日检查资源是否满足要求。第6 d资源需要量超过了限量，即14＞10，故要调整。第6 d共有3项工作：③—⑤，③—④，②—④。这3项工作的最早完成时间与最迟开始时间如表5.42所示。

表5.42　3项工作时间表（2）

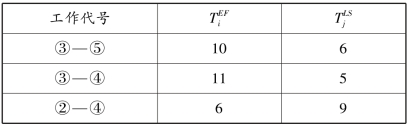
由表5.42中时间参数判断，的最大值和的最小值属于同一项工作②—④，所以分别找的次大值和的次小值所对应的工作是③—⑤工作。因为=6-6=0小于，所以将③—⑤工作移动到②—④工作之后进行。移动后的时标网络计划图及资源需要量曲线如图5.55所示。

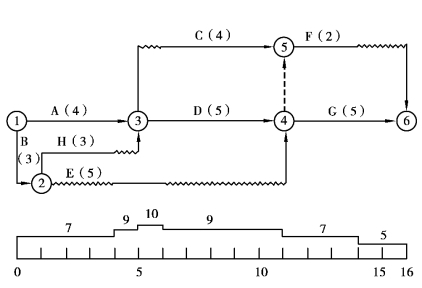
图5.55　移动结束后的时标网络及资源需要量曲线(www.xing528.com)

至此，资源需要量已满足供应的要求，并且在优化过程中工期未延长。

【任务28】 某工程由表5.43所列的工程活动组成，试完成以下任务：

①绘制一般双代号网络图；

②计算各节点时间参数；

③确定总工期及关键线路；

④绘制时标网络图；

⑤绘制劳动力资源需要量曲线；

⑥如果劳动力限制为20人，请寻找新的工期安排。

表5.43　工程活动逻辑关系表

3）工期-成本优化

工程成本由直接费和间接费组成。直接费由人工费、材料费和施工机械使用费组成。施工方案不同，直接费也就不同；但施工方案一定，工期不同，直接费也不同。间接费一般随工期的增加而增加。考虑工程成本时，还应考虑到拖延工期要接受惩罚，提前完工会得到奖励，提前投入使用会带来经济效益。工程成本与工期的关系如图5.56所示。

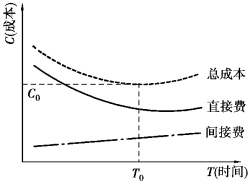
图5.56　工期-成本关系曲线

工期-成本优化的目的是：求出与最低工程总成本C0相对应的工程总工期T0，或规定工期条件下的工程最低成本。网络计划工期的长短取决于关键线路的持续时间。关键线路由关键工作组成。为使工期-成本优化，必须研究分析网络计划中工作工期和费用（主要是直接费）之间的关系。

工期-成本优化的程序如下：

第1步，绘制正常时间下的网络计划。

第2步，求出网络计划图中各项工作采取可行方案后可加快的时间。

第3步，求出正常工作时间和加快工作时间下的工程直接费，并求出费用变化率：

式中 CB——加快工作时间下的费用；

CA——正常工作时间下的费用；

tB——加快的工作时间；

tA——正常的工作时间；

ai-j——i-j工作的费用变化率。

第4步，寻求可以加快的工作。这些工作应满足3个条件：它是一项关键线路上的关键工作；它是可以压缩的工作；它的费用变化率在可压缩的关键工作中是最小的。

第5步，确定本次压缩可以加快多少时间，增加多少费用，主要通过以下标准进行决策：

①如果网络计划图中有几条关键线路，则几条关键线路都要压缩，并且压缩相同的数值，而压缩的时间是几条关键线路中可压缩量的最小值。

②每次压缩以非关键线路转化为关键线路为度。

第6步，以所选可加快的工作及时间为限制，逐个加快工作，每加快一次都要重新计算时间参数，用以判断下次加快的幅度，直至出现下列情况之一为止：

①一条关键线路上所有工作的可压缩时间已全部用完时。

②因工作加快而增加的直接费开始超过因提前完工而节约的间接费时。

第7步，求出优化后的总工期、总成本，绘制工期-成本优化后的网络计划图。

【案例5.28】 图5.57为某工程的网络计划图及其正常作业时间的算例。表5.44中是它的原始资料，经计算可得出第9栏的数字。要求进行工期-成本优化。

图5.57　某工程的网络计划图

表5.44　赶工费率表

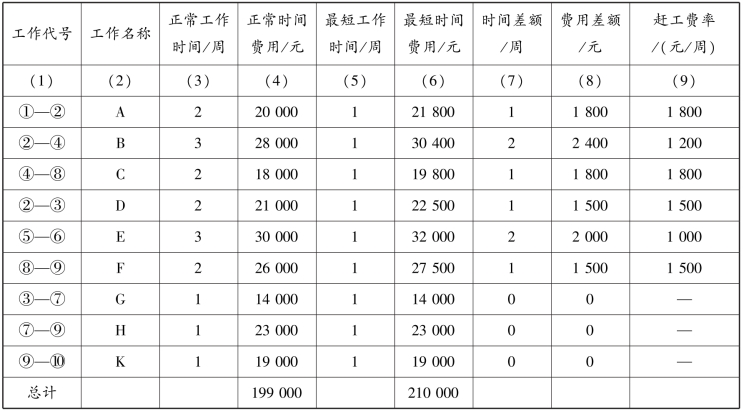
第1步，根据表中所给原始资料，求得费用变化率（赶工费率）。即：

第2步，寻找可以加快的工作。

①计算各节点时间参数，如图5.58所示，求得A、B、E、F、K工作是关键线路上的关键工作。

②K工作是不可压缩的。

③E工作赶工费率最小，所以先压缩E工作。

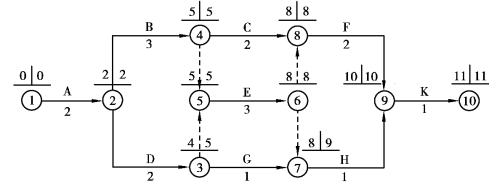
图5.58　计算节点时间参数的网络图

第3步，判断E工作可以压缩多少。虽然E工作有可压缩时间2周，但压缩1周后，C工作转化为关键工作，关键线路增加。若要再压缩，E、C工作要同时压缩，这时赶工费率就不是最小的，所以E工作压缩1周。同理，依次判断各项关键工作，过程列于表5.45中。

表5.45　判断各项关键工作压缩量

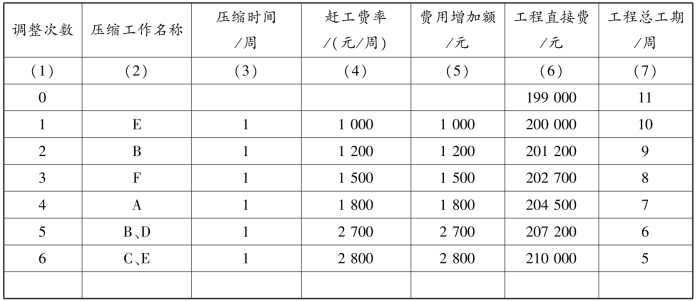
至此，各条线路均变成关键线路，各项工作的压缩时间已用完，故压缩停止。

第4步，假定每周工程间接费为1 600元，则网络计划的总成本如表5.46所示。

表5.46　网络计划费用及成本

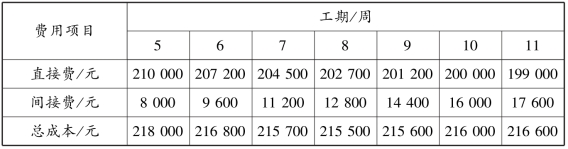
由表5.46可见，工期为8周时的总成本最低。

将优化过程所得的各项费用绘制成工期-成本曲线，如图5.59所示。

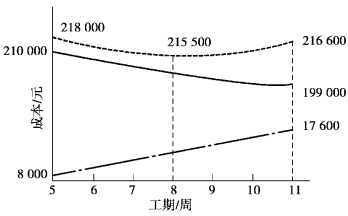
图5.59　优化后的工期-成本曲线

第5步，绘制工期-成本优化后的网络计划图（图5.60），付诸实施。

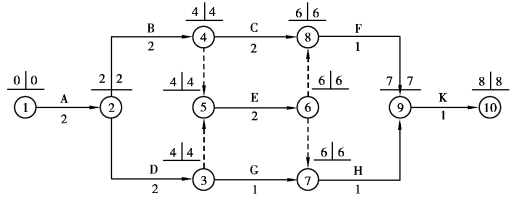
图5.60　优化后的网络计划图

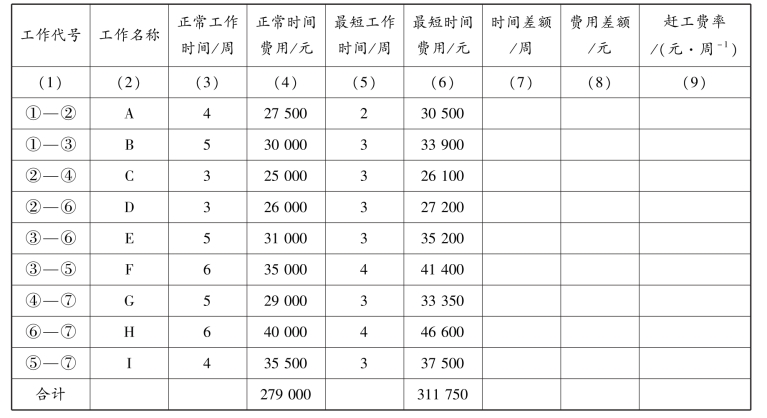
【任务29】 图5.61为某工程的网络计划图及其正常作业时间的算例。表5.47中是它的原始资料，要求进行工期-成本优化。

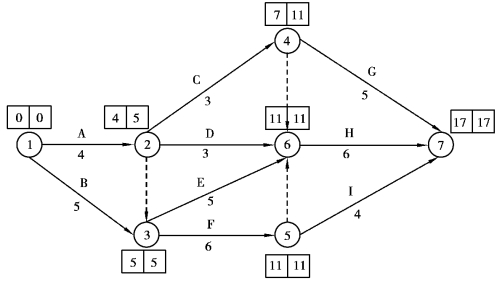
图5.61　某工程的网络计划图

表5.47　赶工费率表