无节拍流水作业施工次序的确定-公路工程施工组织设计成果

公路工程施工由于受作业条件、工程复杂程度及外界因素的影响，流水作业并不会按理想的状态有规律地进行，而最为常见的是无节拍的流水作业。在前面已经提到，在确定无节拍流水作业的施工总工期时，必须先对施工段排定施工次序，否则，将不能求得最短施工总工期。

如果有m个施工段，每个施工段都有n道施工工艺相同的工序，那么，怎样安排各个施工段的施工次序，才能使总工期最短呢？这里所指的m个施工段，是指那些施工内容相同的单位工程或分部、分项工程。

1）m个施工段2道工序的施工任务次序的确定

对于这类问题可以用约翰逊-贝尔曼法则来解决。此法则的基本思想是：先行工序施工工期短的要排在前面施工，后续工序施工工期短的要排在后面施工。首先列出2道工序在m个施工段的“流水节拍表”，然后在表中依次选取最小数，而且每列只选一次。若此最小数是先行工序在某施工段的流水节拍值，则此施工段的任务排在前面开工，反之，若此最小数是后续工序在某施工段的流水节拍值，则此施工段的任务排在后面开工。具体步骤通过示例详解如下。

【案例5.7】 某施工任务可划分为5个施工段，按施工工艺流程每个施工段由两道工序完成，即挖基和砌基，流水节拍如表5.8所示。

①填列“流水节拍表”，如表5.8所示。

②绘制“施工次序排列表”的表格，如表5.9所示。

表5.8　某施工项目流水节拍表　单位：d

表5.9　施工次序排列表

③填表排序。即按约翰逊-贝尔曼法则的基本思想完成表5.9，从而可将各施工段的施工次序排列出来。

本示例中，根据表5.8，各施工段的施工次序排列如下：

在表5.8中首先选取最小数1，此最小数是后续工序在D施工段的流水节拍值，则D施工段的任务排在后面开工，即排在第6位，将D施工段填入表5.9相应的格子中。因为D施工段的次序已确定，所以再次选择最小数时，D列的“8”不作为比较的对象，即每列只选一次，下同。再次选取最小数2，此最小数是先行工序在F施工段的流水节拍值，则F施工段的任务排在前面开工，即排在第1位，将F施工段填入表5.9相应的格子中，下同。依次选取最小数3，此最小数是先行工序在E施工段的流水节拍值，则E施工段的任务排在前面开工，即排在第2位。依次选取最小数4，此最小数既是先行工序在A和B施工段的流水节拍值，又是后续工序在B施工段的流水节拍值，此时不能只依据先行工序或后续工序来判定施工段开工的前后次序；这时可以通过计算完成一个施工段花费总时间的长短来确定施工段开工的前后次序，即完成A施工段需花费时间为4+7=11（d），完成B施工段需花费时间为4+4=8（d），因为11 d＞8 d，所以把花费时间长的A施工段排在前面开工，即排在第3位，把花费时间短的B施工段排在后面开工，即排在第5位。最后，C施工段排在第4位。

④按照最优施工次序绘制施工进度横道图，确定施工总工期。为便于作图，按各施工段最优施工次序，重列各工序流水节拍表，如表5.10所示。

表5.10　按最优施工次序排列的流水节拍表　
单位：d

按表5.10中施工段的最优施工次序绘制施工进度横道图，并确定总工期，如图5.11所示，其总工期为28 d。若不按约翰逊-贝尔曼法则所确定的施工次序，不一定能取得最短施工总工期。如本示例中，若按表5.8的施工次序，即按A、B、C、D、E、F的次序施工，则总工期至少需要34 d，比最短施工总工期28 d多6 d。

图5.11　最优施工次序流水作业施工进度横道图

【任务8】 在案例5.7中，请按表5.8的施工次序绘制施工进度横道图（注意：有两种思路，即专业队连续作业组织施工和紧凑法组织施工，可得工期分别为T1和T2）。

【任务9】 在案例5.7中，请按表5.10的最优施工次序绘制施工进度横道图（注意：有两种思路，即专业队连续作业组织施工和紧凑法组织施工，可得工期分别为T3和T4）。

思考：任务8中的T1和T2与任务9中的T3和T4有什么关系？哪个施工总工期最长？哪个施工总工期最短？为什么？

2）m个施工段3道工序的施工任务次序的确定

对于这类问题，如果符合下列两种情况中的一种，就可以采用约翰逊-贝尔曼法则，这两种情况是：

①第1道工序中最小的工序工期tamin大于或等于第2道工序中最大的工序工期tbmax，即tamin≥tbmax；

②第3道工序中最小的工序工期tcmin大于或等于第2道工序中最大的工序工期tbmax，即tcmin≥tbmax。

对于m个施工段3道工序的施工任务次序的排序问题，只要符合上述两种情况中的一种时，即可按以下示例中的具体步骤来求得最优施工次序。

【案例5.8】 某施工任务为拱涵基础施工，共5座拱涵，每座拱涵基础施工分解为3道工序，即开挖、砌筑和回填，流水节拍如表5.11所示。

表5.11　某施工任务流水节拍表　单位：d

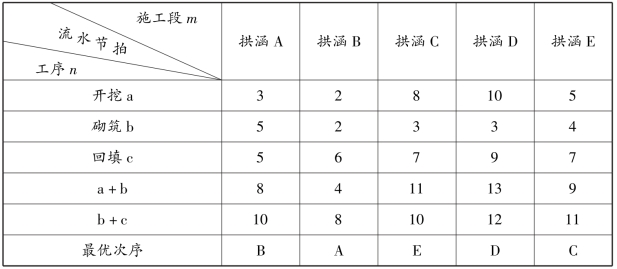
因为a工序中最小的工序工期tamin=2小于b工序中最大的工序工期tbmax=5，条件不满足；而c工序中最小的工序工期tcmin=5等于b工序中最大的工序工期tbmax=5，即tcmin≥tbmax条件满足。所以，可以采用约翰逊-贝尔曼法则排定施工任务最优次序，具体步骤如下：

①将各个施工段中第1道工序a和第2道工序b的流水节拍（工序工期）分别相加，即工序a+b，ta+tb；

②将各个施工段中第2道工序b和第3道工序c的流水节拍（工序工期）分别相加，即工序b+c，tb+tc；

③将上两步中得到的流水节拍表（工序工期表）看作两道工序（即a+b和b+c）的流水节拍表（工序工期表），如表5.11所示。

④按m个施工段2道工序时的施工任务次序排定方法，求出最优施工次序，如表5.12所示。(www.xing528.com)

表5.12　施工次序排列表

⑤按所排定的施工次序绘制施工进度横道图，确定施工总工期。

为便于作图，按各施工段最优施工次序，重列各工序流水节拍表，如表5.13所示。

表5.13　按最优施工次序排列的流水节拍表　单位：d

本示例按上述方法排定的最优施工次序为B、A、E、D、C。

【任务10】 在案例5.8中，请按表5.11的施工次序，分别以紧凑法和专业队连续作业绘制施工进度横道图，并确定总工期。

【任务11】 在案例5.8中，请按表5.13的最优施工次序，分别以紧凑法和专业队连续作业绘制施工进度横道图，并确定总工期。

3）m个施工段多于3道工序的施工任务次序的确定

如果m个施工段3道工序（不满足上述特定条件）或者m个施工段多于3道工序的施工任务，应如何确定最优施工次序呢？

对于这种情况，应采用穷举法，找出最优施工次序。即还是按照前述思路，将工序重新组合成2道工序（包括所有可能的情况），再按约翰逊-贝尔曼法则确定各种组合对应的最优施工次序。接着，按紧凑法（或开工要素法）组织施工的思路求得各组合最优施工次序下的最短施工总工期（可借助直接编阵法，不用绘制施工进度横道图）。最后，比较各组合对应的最短施工总工期，最小值就是完成该施工任务真正的最短施工总工期，对应的施工次序即为完成该施工任务的最优施工次序。具体步骤详见案例5.9。

【案例5.9】 表5.14所示为4个施工段3道工序的施工任务次序的确定。

分析：由表5.14可知，a工序最小的工序工期3小于b工序最大的工序工期6，c工序最小的工序工期5也小于b工序最大的工序工期6，所以，此案例属于m个施工段3道工序不满足前述特定条件的施工任务次序的确定问题。

最优施工次序确定步骤如下：

①将a、b、c 3道工序重新组合成2道工序（包括了所有组合情况），见表5.15中组合1（a，b+c）；表5.16中组合2（a+b，c）、表5.17中组合3（a+c，b）、表5.18中组合4（a+b，b+c）、表5.19中组合5（a+c，b+c）。

注意：先行工序和后续工序的位置不能颠倒，即（b+c，a+c）、（a+c，a+b）、（c+b，c+a）等组合都是错误的。

②按约翰逊-贝尔曼法则分别确定组合1～5对应的最优施工次序，如表5.15—表5.19所示。

③用直接编阵法求得组合1～5最优施工次序下的最短施工总工期，如表5.15—表5.19所示。其中，组合1～5对应的最优施工次序下的最短施工总工期都是35 d；而默认次序：A、B、C、D的最短施工总工期是37 d，如表5.20所示。

表5.14　某施工任务流水节拍表　单位：d

表5.15　组合1：流水节拍表　单位：d

表5.16　组合2：流水节拍表　单位：d

表5.17　组合3：流水节拍表　单位：d

表5.18　组合4：流水节拍表　单位：d

表5.19　组合5：流水节拍表　单位：d

表5.20　默认次序流水节拍表　单位：d

由表5.15—表5.20可以得出，该施工任务的最短施工总工期是35 d。最优施工次序是：C→B→A→D、C→D→B→A、C→B→D→A、B→C→D→A。