柱壳结构自由振动特征的计算结果表明,借助当前的数值计算平台,能够建立起可信的加肋柱壳结构的有限元数值平台,在低于500 Hz频率范围内,能够进一步用于分析其强迫振动响应和辐射噪声特征。在此基础上,采用同样的计算方法分析加肋锥壳结构的自由振动特征。因加肋锥壳结构对应为艇尾舱段,较为敏感,试验数据非常稀少。校验对象取为拥有理论解的加肋圆锥壳模型,大端半径为3.5 m,小端半径为1.75 m,圆锥壳轴线长度为10.8 m,壳体厚度为0.016 m,均匀布置矩形截面的17根内环肋,环肋高度为0.25 m,厚度为0.014 m,锥壳和环肋均采用钢材料,弹性模量为2.1×1011Pa,泊松比为0.3,密度为7 800 kg/m3。
锥壳同样以壳单元进行离散,肋骨梁单元与壳单元相交于锥壳几何中面。网格单元尺寸仍取为Δ/2,内部充满水时,网格节点总数为38.8万个。流固耦合自由振动分析在24核、CPU主频2.4GHz、24G内存的工作站上计算,耗时约5 h。计算得到两端简支、两端固支和两端自由三种典型边界条件下的加肋锥壳结构自振频率与理论解比较如表8.23~表8.25所示。可以看出,对于典型的简支和固支边界条件而言,环肋锥壳自由振动频率与解析子结构法理论解之间的偏差小于6%。当锥壳内部充满水时,计算得到两端简支边界条件下的环肋锥壳自振频率如表8.26所示,环肋锥壳干、湿模态振型比较如图8.104所示。可以看出,湿模态频率与理论解之间的偏差控制在8%以内。静流体载荷作用对环肋锥壳自振频率的影响幅度较环肋柱壳要小,并且对模态振型排列秩序的影响程度也更小,仅有局部模态振型呈现错序排列。由上述分析可以得出以下四点结论:

图8.104 环肋锥壳干模态与单边有水时湿模态振型比较
(1)当前使用数值研究工具能够建立起可信的典型加肋柱壳和锥壳结构的有限元数值分析平台,空气中振动响应分析的截止频率可以达到2 k Hz,单边及双边有水情况下的流固耦合自由振动分析在500 Hz频段范围内可以有效保证计算精度。
(2)壳体结构流固耦合自由振动分析时可以采用实体单元离散,也可以采用壳单元离散的方法。前者精度略高,能够有效保证求解收敛的频带范围更宽,但工作量更大。
(3)单边有水情况下的壳体结构流固耦合振动分析可以转换为分析壳体内部填充水时的自由振动特征,转换时应保证两者流固耦合湿表面积相等,如半浸水和半充满水,以此有效减小计算量。
(4)环肋和静流体载荷对壳体结构自由振动特征的影响明显,环肋使柱壳自振频率增加,静流体载荷使柱壳自振频率减小且影响幅度更大,两者均会使得柱壳模态振型呈现错序排列。流固耦合效应对无肋柱壳和环肋柱壳自振频率的影响效果相当。柱壳双边有水相对于单边有水情况而言,自振频率进一步减小,模态振型基本不变。流固耦合效应对环肋锥壳自振频率和模态振型的影响幅度较对环肋柱壳要小。
表8.23 两端简支加肋锥壳结构干模态频率计算(https://www.xing528.com)

表8.24 两端固支加肋锥壳结构干模态频率计算

表8.25 两端自由加肋锥壳结构干模态频率计算

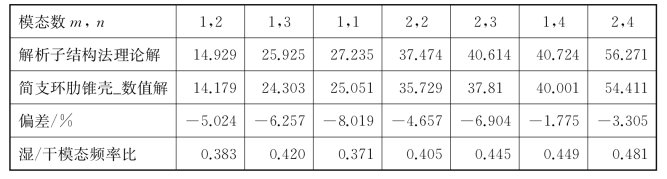
表8.26 两端简支加肋锥壳结构湿模态频率计算
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




