前文计算阐述了柱壳结构在空气中自由振动分析时能够兼顾计算精度的截止频率,但实际艇壳结构振动发声时始终存在单边有水的物理条件,必须考虑流固耦合效应对结构振动和辐射噪声的影响。同时,需要明确评估考虑流固耦合效应时影响结构振动响应计算精度的相关因素。流固耦合是多物理场分析对象中的典型代表,通常所述的流固耦合多指单向耦合,即结构表面的流体载荷作为激励源,改变了结构自身的质量阵和刚度阵,进而改变了结构的振动响应,但由于流体载荷引起的结构形变的量通常较小,结构表面形变对流体流动控制方程求解的影响非常小,通常不予考虑。对于大尺度、刚度较大的舰艇结构振动响应分析而言,该假定通常是合理的。应用该方法分析结构振动特征时,主要有两个因素影响计算精度:一是流固耦合面的网格节点匹配和数据传递;二是附连水质量的区域大小,即附连水质量的大小。当附连水区域过大时,网格节点数迅速增加,严重影响计算耗时;过小时,弱化了流体载荷效应,会降低结构振动的计算精度。因此,有必要分析柱壳结构在单边有水以及更为复杂的双边有水情况下的自由振动特征,以此来摸索内在规律。
当柱壳双边有水时,需要引入两个流固耦合交界面进行数据传递。此时,能否采用常规的壳单元离散的分析思路仍没有统一的说法。当前,在经典ANSYS结构分析中有两种思路解决该问题:一是在几何建模时将柱壳描述为实体结构,然后以实体单元来离散柱壳,进而控制双面流固耦合;二是仍将柱壳描述为指定厚度的壳体结构,并以壳单元进行离散,但指定两次流固耦合交界面时需要首先将壳单元网格节点全部复制,然后进行两次赋值。第一种方法不仅大大增加了几何建模的工作量,而且使得进行结构化网格离散时难度增加,网格节点数也明显增加,加重了计算负担,特别是对于加肋柱壳复杂结构而言更是如此。第二种方法中柱壳自身的网格离散相对于空气中自由振动分析时并未改变,在计算资源一定的情况下,可以将主要精力集中于流体网格实体节点和流固耦合交界面的求解上,分析策略更为合理,但是该分析方法的计算精度尚无明确结论,尚需进行校验。因此,本案例的研究目的一方面是摸索单边有水及双边有水情况下流固耦合振动响应的计算方法,另一方面是摸清流固耦合交界面数据传递和附连水区域大小对计算精度的影响。
校验对象三为两端封闭的简支钢制圆柱壳,长为1 284 mm,外半径为180 mm,板厚为3 mm。壳体材料属性如下:弹性模量为2.07×1011Pa,泊松比为0.29,密度为7 750 kg/m3。该对象浸没于水深为1.6 m的水池中的湿模态响应试验测量由西伦敦大学和皇家海军学院联合完成,试验测量现场如图8.97所示。

图8.97 柱壳单边有水时湿模态测量试验布置
自行数值计算时,首先,以实体单元来离散柱壳几何参数,并且分析柱壳在内部充满水情况下的湿模态响应。该计算设置的考虑在于期望避开流体区域大小对计算精度的影响问题,而且无须引入无穷远处声吸收面边界条件。在考虑流固耦合效应前,首先也需要校核柱壳干模态的计算精度。但是,与前2个分析对象中计算设置不同的是,将柱壳内部空间设定为空气区域,并且引入流固耦合交界面,用于分析气-固耦合作用下的壳体自由振动特征。在此基础上,只需将流体域的介质参数由空气变为水,即可分析柱壳在单边有水情况下的湿模态特征。柱壳和内部空气域的实体单元离散如图8.98所示。网格尺寸按前述经验取为Δ/2,网格节点数为16.7万个。
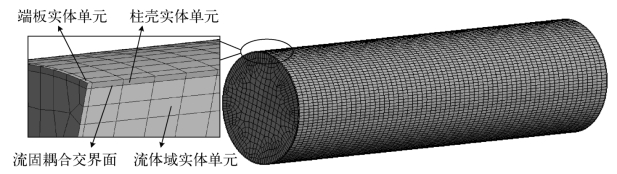
图8.98 柱壳实体网格单元离散时有限元网格布置
计算得到柱壳干模态和湿模态频率与试验值的比较如表8.14所示。可以看出,流固耦合效应已经体现在结构振动方程求解的结果中。当内部流体介质为空气时,柱壳自振频率的最大计算误差为3.6%;当流体介质为水时,柱壳湿模态频率的最大计算误差为5.2%,满足当前工程精度要求。此时,在流体静载荷作用下,柱壳自振频率减小,湿模态频率与干模态频率之比约为0.6,而且模态振型排列次序发生了改变。计算得到的柱壳干模态振型与皇家海军工程学院研究人员的有限元计算结果比较如图8.99所示,柱壳湿模态与干模态振型比较如图8.100所示。可以看出,干模态振型能够与第三方解吻合一致,湿模态振型也能够清晰再现柱壳的自由振动特征。
表8.14 柱壳实体单元离散时干、湿模态频率计算校验

续 表


图8.99 柱壳实体网格单元离散时干模态振型计算校验

图8.100 柱壳实体网格单元离散时湿模态与干模态振型比较(https://www.xing528.com)
鉴于该柱壳湿模态试验测量是在全浸没于水中完成的,与水接触的面为柱壳外表面,而上述数值计算分析的对象为柱壳内部充满水,与水接触的面为柱壳内表面,两者略有差异,需要进一步讨论该转换分析思路的合理性。为此,进一步分析柱壳全浸没于水中的自由振动特征,此时柱壳内部为空气介质。参照现有螺旋桨流固耦合振动分析时附连水区域通常取5倍桨叶直径的分析经验,分别在柱壳外围建立大、小两个水体区域,水体径向直径分别为4D和2.2D(D为柱壳直径),同样采用结构化实体网格单元来离散柱壳和水体区域,两者网格节点数分别为26.88万个和17.48万个,对应为G1和G2。计算时,除引入柱壳外表面与水接触的流固耦合交界面外,还引入水体外围吸声边界条件,声速为0,以模拟无穷大水域情况。计算得到柱壳在全浸没于水中时的自振频率与试验值的比较如表8.15所示。可以看出,当附连水区域大小增加约1倍时,柱壳一阶自振频率计算值的变化幅度达到了2.8%,其余主要自振频率变化量约为1%,由此表明:当分析对象尺寸较大、计算资源难以满足要求时,有效考虑流固耦合振动响应的外围径向水域大小至少应为特征直径的2倍。当取为3倍特征直径大小时,基本能够满足计算精度要求,比现有经验中的5倍水体直径略小。此时,计算得到的柱壳湿模态频率与全充满水条件下的结果几乎重合,既说明了采用实体单元有限元离散柱壳以求解其自由振动的有效性,也证明了前述转换分析思路的合理性。
表8.15 柱壳浸没于水中时湿模态频率计算校验

在此基础上,将柱壳内部空气介质改为水,以考虑柱壳双边有水情况下的流固耦合振动响应,外围水体径向大小取为3D,分析时同时考虑网格密度对计算精度的影响。建立密、疏两套结构化有限元网格,网格节点数分别为23.93万个和14.47万个,分别对应为G3和G4。两套网格的差异体现在柱壳周向和轴向网格单元数同时减小,G4基本满足网格单元尺寸为Δ的要求。计算得到柱壳双边有水时的湿模态频率与单边有水模态频率试验值的比较如表8.16所示,湿模态振型与全浸没时振型的比较如图8.101所示。可以看出,在网格节点数增加约10万个时,自振频率几乎不变。双边有水相对于单边有水而言,自振频率进一步减小,平均约为单边有水自振频率的76%。在排除附连水区域大小和网格密度影响的情况下,取G1和G3网格计算结果,得出结论如下:①采用实体网格单元离散的方法来分析柱壳单边以及双边有水条件下的流固耦合振动响应是可行的;②柱壳单边有水情况下的自由振动分析可以转换为分析内部充满水的情况,与全浸没于水中时自振频率相同,模态振型也相同;③柱壳双边有水相对于单边有水而言,自振频率减小为约76%,模态振型不变。
表8.16 柱壳双边有水时湿模态频率计算分析

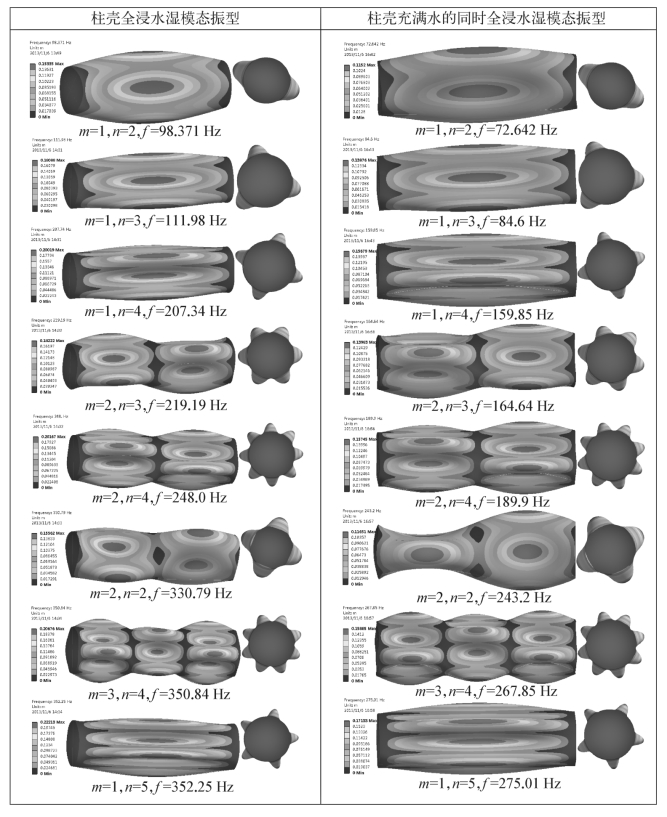
图8.101 柱壳单边有水和双边有水时湿模态振型比较
需要注意的是,以内部充满水的物理条件来分析壳体单边有水时的流固耦合自由振动特征时,无法考虑小水深条件下的声自由液面影响。为了解决这一问题,进一步分析柱壳半充满水和半浸没于水中的自由振动特征,以找出两者之间的内在联系。分析时柱壳仍以实体单元进行离散。当内部半充满水时,内部同时存在水和空气两种流体介质,存在两个流固耦合交界面,需要引入声压为0的声自由液面边界。当柱壳半浸没于水中时,同样存在气-固和水-固两个流固耦合交界面,需引入声自由液面和水体外围吸声边界条件。此时,计算域网格节点分布完全与G4相同,节点数仍为14.47万个。计算得到两种条件下柱壳自振频率如表8.17所示,两种条件下模态振型比较如图8.102中所示。可以看出,与全充满水相比,半充满水和半浸没于水中时柱壳自振频率均增加,且变化幅度较为稳定,约增加为全充满水时的1.2倍,模态振型基本不变,但局部振型排列次序发生改变。此时,柱壳模态振型在周向上的对称特征被弱化,与水接触面的变形量并不等同于与空气接触面的形变。从试验得出的8阶模态数来看,半充满水与半浸没于水中两种条件下的柱壳自振频率和模型振型几乎重合,半充满水条件下仅未能捕捉到半浸没于水中时表现出的第(2,2)阶模态。由此表明,半浸没时自由振动分析也可以转换为半充满水的条件,与全浸没时一致。由此表明:柱壳单边有水条件下的自由振动分析可以针对内部填充水来完成。由浸没水转换为填充水时,两者液面高度应相等,且部分充满水时同样要考虑声自由液面影响。
表8.17 柱壳实体单元离散时计算半浸没水和半充满水条件下的湿模态频率

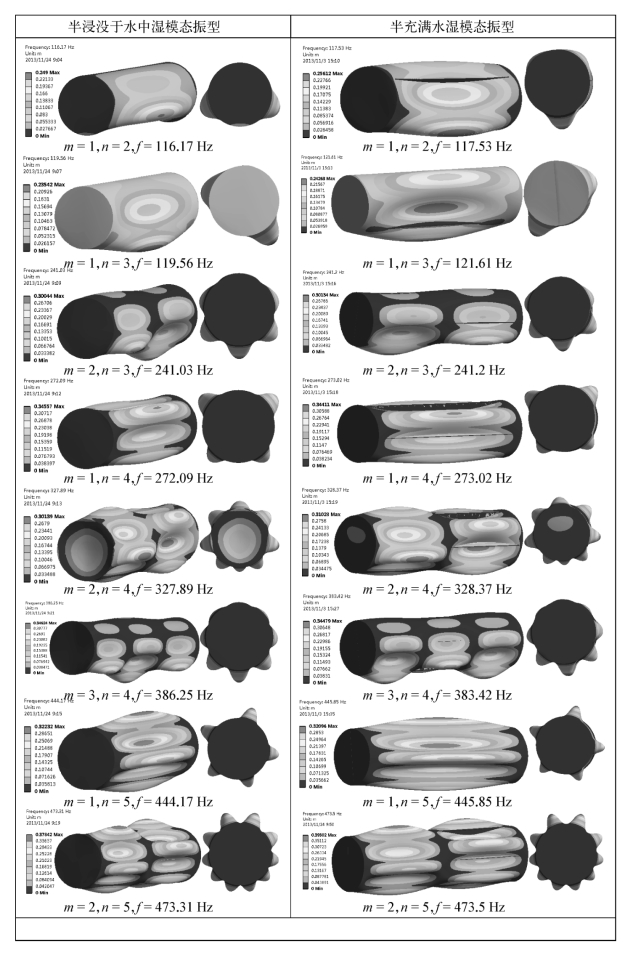
图8.102 柱壳实体单元离散时半充满水与半浸没于水时的湿模态振型比较
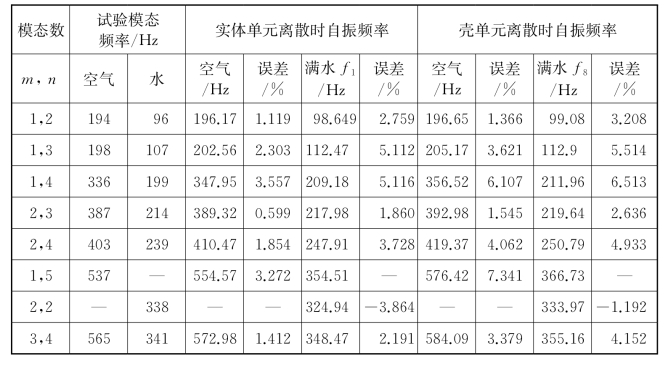
在上述解决柱壳单边及双边有水条件下的流固耦合自由振动分析的基础上,为了减小复杂锥-柱-球组合壳体结构振动分析的计算难度和计算量,还应探索柱壳在壳单元离散时流固耦合振动计算的可行性,并进一步扩展到加肋柱壳和加肋锥壳的自由振动特征分析上来。柱壳壳单元离散时较实体单元离散更为简单,网格单元尺寸仍取为Δ/2。内部充满水时,网格节点总数为20.47万个,与前文分析相当。柱壳壁面采用结构化网格分布,流固耦合面计算设置与前述相同。计算得到该柱壳干、湿模态频率与试验值及实体单元离散时的计算结果的比较如表8.18所示。可以看出,壳单元离散方法对于柱壳单边有水情况下的流固耦合自由振动分析同样有效,自振频率的计算精度较实体单元离散时下降约1%,收益是计算耗时减小。存在的问题如下:当模态阶数较高、频率达到中高频段时,计算容易出现收敛性问题,在网格离散时需要重点关注网格质量,特别是两端封闭面上的网格单元。
表8.18 柱壳壳单元离散时干、湿模态频率计算校验
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




