艇模阻力数值计算确认分析：可信性研究

分析载体为标模SUBOFF潜艇，该潜艇具有全套水动力试验数据，便于开展泵喷推进系统设计与试验测量。鉴于潜艇主推进器从7叶桨到泵喷的更新换代，推进器并非孤立存在，而是与艇尾构型高度集成设计，如美国“海狼级”和“弗吉尼亚级”泵喷推进潜艇均采用木字形艇尾，法国“凯旋级”潜艇采用H形艇尾，甚至国外某型潜艇采用米字形艇尾，且船坞中“弗吉尼亚级”潜艇SSN-789尾锥段的小端与大端直径比大于0.35，明显与当前现役的十字形尾翼-7叶桨结构匹配特征不同，如图8.33所示，围壳及尾翼附体的复杂涡系与伴流特征将直接影响推进器水动力、推进和声学性能，因此泵喷设计时还需完成艇尾结构匹配性设计。其设计准则如下：以艇模阻力、桨盘面湍流涡强度和伴流速度周向不均匀度为优化参数，开展艇尾构型的流体动力性能优化设计研究，主要包括X形、木字形和星形三种结构型式。分析步骤如下：首先基于无附体光体SUBOFF AFF-1对象和全附体SUBOFF AFF-8对象完成CFD计算可信度的确认分析，然后针对无围壳的不同艇尾构型进行计算分析，最后定量比较带围壳的不同艇尾构型流体动力性能，确定泵喷推进时的较优艇尾构型。

图8.33　典型艇尾构型

（a）“海狼级”潜艇；（b）“弗吉尼亚级”潜艇；（c）“凯旋级”潜艇艇尾；（d）某潜艇艇尾；（e）SSN-789“弗吉尼亚级”潜艇艇尾

分析对象取为美国国防高等研究计划署（Defense Advanced Research Projects Agency，DARPA）发布的标准潜艇SUBOFF模型，美国大卫·泰勒研究中心（David Taylor Research Center，DTRC）针对该潜艇给出了众多水动力试验数据，包括阻力曲线、艇体表面压力系数分布和摩擦阻力系数分布等。SUBOFF模型总长4.356 m，其首部长为1.016 m，平行中体长为2.229 m，尾部长为1.111 m，平行中体最大直径为0.508 m。带指挥台围壳时，围壳0.206 m、长0.368 m、最大厚度0.066 m。尾翼端面高0.25 m、轴向长度0.095 m，如图8.34所示。

图8.34　SUBOFF潜艇模型几何尺寸

为了充分研究该艇光体及附体的阻力性能，包括摩擦阻力和压差阻力分量的变化规律，DARPA将该标准潜艇定义为一个系列，并依据不同部件组合给予命名，包括光体AFF-1、光体+围壳AFF-2、光体+十字形尾翼AFF-3、光体+围壳+十字形尾翼AFF-8（亦称为全附体潜艇）、光体+十字形尾翼轴向前移3%L（L为艇长）AFF-10以及光体+环形导管AFF-6等，如图8.35所示。X形翼由原十字尾翼周向旋转45°得到，木字形翼由原十字形尾翼和X形翼轴向前移3%L后组合得到，星形翼由X形翼和原十字形尾翼轴向前移3%L后组合得到，如图8.36所示。

图8.35　SUBOFF潜艇模型系列几何形状

（a）AFF-1；（b）AFF-2；（c）AFF-3；（d）AFF-10；（e）AFF-8

图8.36　SUBOFF潜艇典型艇尾构型

（a）X形翼；（b）木字形翼；（c）星形翼

在进行CFD计算可信度校验分析时，主要针对AFF-1和AFF-8几何形状完成，包含其他组合式对象。艇体计算域采用多块六面体结构化网格进行离散，如图8.37所示，即使是全附体艇体复杂几何形状，其网格最小正则度指数也大于0.3，而对于对称几何形状AFF-1，网格最小正则度指数甚至高达0.7，能够有效保证计算迭代收敛。其中，光体全六面体网格节点数为288万个，全附体潜艇网格节点数为682万个。艇体壁面径向方向、艇首、指挥台围壳和尾附体的翼型四周均采用O形网格，以尽可能捕捉流动变化剧烈的局部细节。流场控制域取为艇体上游方向1L、下游方向2L、径向方向10D（D为艇体平行中体最大直径）。计算时取为均匀来流速度进口和压力出口边界条件，初始湍流强度取为5%，并考虑潜艇轴向沉深10 m产生的静压。

图8.37　SUBOFF潜艇结构化网格拓扑和壁面网格单元

（a）光体AFF-1，网格节点数为288万个；（b）光体+围壳+尾翼AFF-8，网格节点数为682万个

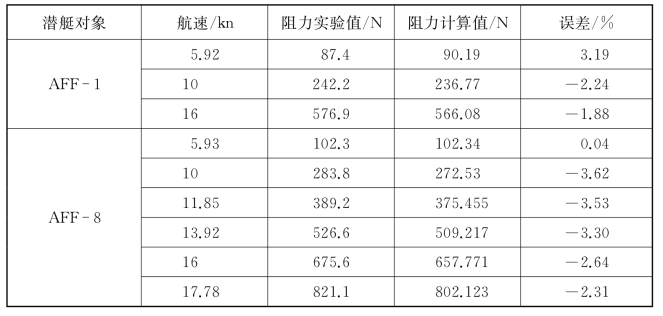
计算得到低、中、高三种航速下AFF-1阻力值以及不同航速下AFF-8阻力曲线与试验值的比较如表8.3所示。可知，在全航速范围内，光体和全附体总阻力的CFD计算误差小于3.6%，能够用于后续的优化设计分析。下面着重针对AFF-8几何形状，分析网格拓扑一定的情况下，网格节点空间分布规律和求解程序/软件对计算精度的影响，总结艇模阻力CFD计算可信性确认的主要因素，为艇尾构型流体动力优化设计作铺垫。

表8.3　AFF-1阻力和AFF-8阻力曲线计算值与试验值的比较

采用O形网格拓扑包裹艇体黏性绕流且控制计算域离散结构化网格质量相当的情况下，典型网格节点空间分布规律因素改变后的艇体壁面结构化网格如图8.38所示，包括网格节点数量、网格节点疏密分布规律和第一层网格节点法向距离因素，命名四组六面体网格为G1、G2、G3、G4。G1和G2均对应中等网格节点数，在艇首段、尾锥段和平行中体段，网格由适应流动变化剧烈程度的疏密相间分布变为均匀分布。G3和G4分别对应为G1在艇体表面流动变化剧烈的局部区域进行稀化和加密处理，表征粗网格和细网格。

图8.38　AFF-8艇体壁面网格

采用SST湍流模型、中等湍流强度的初始进流边界条件，求解时对流项和湍流数值离散均采用高阶精度格式、设置相同的迭代收敛标准，四种网格计算得到的潜艇阻力与实验值及经验公式估算值比较如表8.4所示。其中，Cd和Cf分别定义为

式中，Ds为艇体总阻力；F为摩擦阻力；S为艇体浸湿表面积。ITTC-57、桑海和普朗特Cf经验公式分别对应为

式中，Re为基于航速v和艇长L的雷诺数。形状阻力系数CR=Cd-Cf。

表8.4　潜艇阻力CFD计算值与实验值及经验值比较(www.xing528.com)

可知，从G3到G1再到G4，在同样的网格节点疏密分布规律下，随着网格节点数的增多，计算阻力值减小并逐渐接近真值，计算精度可提高约2%。G4对应的误差小于1%，在工程应用上已具有足够可信度。G1和G2因网格节点数量相同，阻力计算精度相近，但G1形状阻力系数的计算精度高于G2，表明此时网格空间尺度已适合艇体表面流动，均匀分布或适合流动特征的疏密相间分布对总阻力影响不明显。但是，疏密分布从流动特性上来讲要更合理一些。

G4艇体纵中剖面的压力系数Cp轴向分布、网格密度与网格节点疏密分布对壁面压力系数和壁面剪切应力系数Cτ分布的影响如图8.39所示。可知，数值计算值与实验值吻合非常好，且与文献计算值几乎重合，并且在指挥台围壳顶部的计算值稍优于瑞士国防研究中心的计算结果。G4相对于G1在艇首段、尾锥段、围壳和尾翼前缘加密后，Cτ在上述加密部位出现轻微差异，但Cp仅在围壳和尾翼前缘处幅值存在差异，其余部位几乎重合，表明G1的网格量级已能较好地捕捉艇体表面流动。网格节点疏密分布改变后，Cp仅在围壳后缘处和尾锥段前端曲率变化处存在轻微差异，Cτ仅在平行中体段前端存在轻微差异，阐明了改变前后阻力值相近、形状阻力系数存在轻微差异的现象。上述结果中，分析对象均对应为模型尺度，满足SST湍流模型采用修正壁面函数时Y+＜200的要求。网格生成时，可通过经验公式来控制壁面第一层网格节点法向距离Δy，从而有效控制Y+以满足使用条件，如下式所示：

图8.39　艇体壁面压力系数和剪切应力系数分布校验

（a）壁面压力系数校核；（b）网格密度对压力系数的影响；（c）网格密度对剪切应力系数的影响；（d）网格节点疏密分布对压力系数和剪切应力系数的影响

此外，5种常用湍流模型针对G4网格计算得到的总阻力、摩擦阻力系数和剩余阻力系数值比较如表8.5所示。可以看出，SST湍流模型适应性最好，计算精度最高，ω-RSM模型次之，RNG k-ε模型再次之，且与k-ε模型精度相当，与现有经验一致。ω-RSM模型较SST模型计算耗时明显要长，但在计算精度上两者基本处于同一个量级，因此，从工程应用的角度来讲，对于需求大量分析工况的潜艇黏性流场RANS模拟而言，SST湍流模型相对最优。

表8.5　湍流模型对潜艇阻力数值计算的影响

分析潜艇黏性流场的目的一方面在于校验CFD预报的精度，为潜艇流噪声预报提供准确的声源项；另一方面在于求取潜艇伴流速度分布，为艇尾推进器提供周向非均匀进流，以及分析尾翼构型对推进器进流场的影响。G4网格SST湍流模型计算得到的水线方向指挥台围壳截面和上垂直翼截面的压力系数分布与试验值比较如图8.40所示。可知，计算值与实验值吻合很好，且指挥台围壳靠近端面处的计算精度稍高于密西西比大学团队的计算结果［39］，上垂直翼计算精度稍高于瑞士国防研究中心的计算结果［40］。

图8.40　潜艇附体表面压力系数分布

进一步计算得到位于x/L=0.978处的桨盘面处速度等值线分布和速度分量校验如图8.41所示。图中va、vv和vw分别为轴向和其他两个坐标方向的速度分量。可知，尾翼与主艇体结合部诱导的马蹄涡对桨盘面流场存在着明显的影响，使得尾翼对称面所在平面两边产生对旋涡。且在-90°＜θ＜90°范围内，由于围壳的影响，水线面上、下方两组对旋涡并不完全对称，上方涡核中心离r/R=0.25曲线的距离d1较下方涡核要小，表现在r/R=0.25周向方向上场点的轴向速度分量在30°～60°范围内较120°～150°范围内稍大。r/R=0.25曲线上横向和垂向速度分量在峰值处较实验值要小，但峰值变化所处周向位置与实验一致。计算得到的vv/v=0.9的速度等值线所处径向半径稍大于实验值，且总体计算精度与文献计算结果相当。

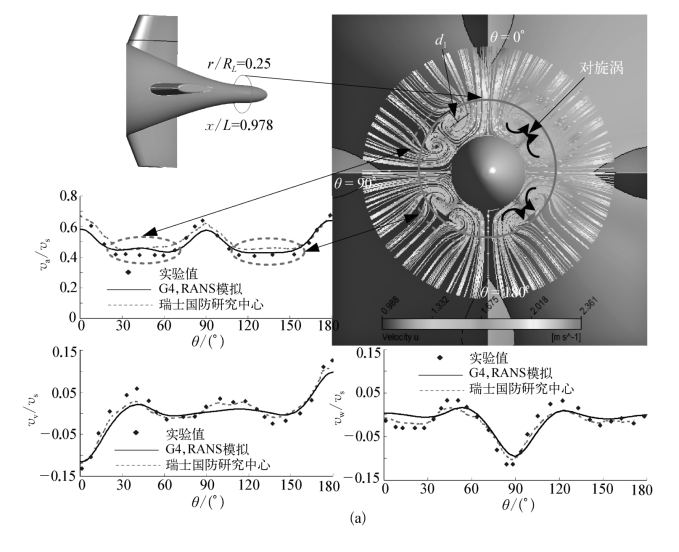
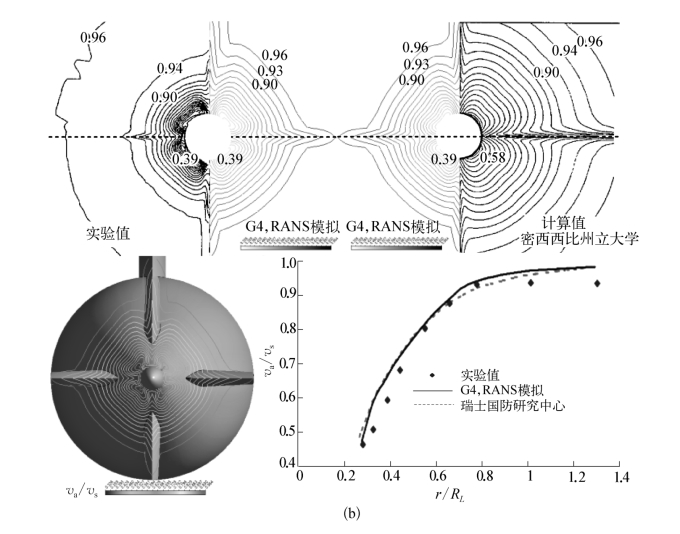
图8.41　潜艇桨盘面速度场校验

（a）速度分量；（b）等值线和周向平均速度

马蹄涡结构是潜艇流场重要的精细流场特征。典型全附体潜艇桨盘面处量纲一的轴向速度分量分布如图8.42所示，包括主艇体与附体尾流及接合部马蹄涡对桨盘面速度分布的影响。通常采用基于速度梯度张量的第二不变量准则（简称Q准则）来定量描述涡量场特征

图8.42　潜艇桨盘面量纲一的速度分布

式中，S和Ω分别为对称张量（流体微团的变形率张量）和反对称张量（流体微团的准刚体转动角速度）。Q反映了流场中流体变形率与转动角速度之间的相对关系，可由此来判定流场中漩涡的形态与位置。

G4网格SST湍流模型计算得到艇体附体及桨盘面的涡量分布如图8.43所示。可知，指挥台围壳和尾翼与主艇体接合部位均产生了马蹄涡，围壳和尾翼的随边下游也均出现了尾涡，且尾涡的影响一直持续到桨盘面处。因尾翼截面通道对流体的挤压作用，同样在下游诱导产生涡。因围壳和上垂直翼上顶端面尾流的同时影响，使得桨盘面处尾流中诱导产生对旋涡。图8.43中潜艇壁面显示为其压力分布。进一步可视化得到潜艇轴向各横截面上涡量分布沿流动方向的演变如图8.44所示。可知，围壳上顶端面涡对沿流动方向持续存在一定距离，几乎不与其他涡系发生相互作用，且不影响半径一定的桨盘面涡量场。

图8.43　AFF-8潜艇G4网格RANS模拟桨盘面涡量分布

图8.44　AFF-8潜艇G4网格RANS模拟涡量分布轴向演变

从前文所述不同航速下总阻力曲线、航速为5.93 kn时艇体壁面及附体表面压力系数、剪切应力系数、桨盘面伴流速度分布以及涡量分布的校验与定量分析可以看出，现有CFD计算方法能够适应艇体黏性绕流精细数值模拟的要求，能够用于艇尾构型基于流体动力性能的优化设计分析。