螺旋桨梢涡流场数值模拟和校验

螺旋桨梢涡精细流场模拟是与梢涡空化初生判定密切相关的热点课题，也是桨叶水动力性能预报的进一步深化应用。桨叶周向旋转过程中，叶尖梢涡流管通常呈漩涡状持续稳定地向下游延伸。鉴于叶梢部位的极小弦长几何参数以及压力面和吸力面之间的压差存在特征，梢涡流管内的流体流动与桨叶主要承载叶截面的流动差异显著，使得其数值模拟难度增加。加之叶梢部位的承载非常小，对桨叶力积分量的影响较弱，使得较多学者在桨叶水动力性能分析时直接将叶梢几何参数进行切割处理，以减小计算难度。从定性分析来看，要想准确、可信地分析螺旋桨梢涡精细流场，除了要保证叶梢几何参数真实外，还必须在原有主要关注桨叶力积分量的数值模型基础上，同时对湍流模型和网格离散加以改进［24-26］。

水动力性能数值预报时，通常采用定常RANS模拟方法，且湍流模型多采用鲁棒性和求解精度均非常好的SST湍流模型，其湍流黏度项μt为

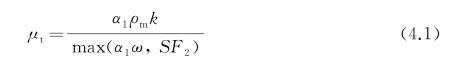
式中，α1=5/9；S为应变率；混合函数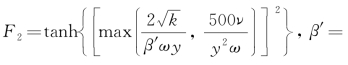0.09，ν为流体运动黏度，y为近壁面距离。在自由流动区域时，F1=0；而在近壁面区域时，F1=1，由低雷诺数公式进行求解。数值模拟时，对这两个区域的界定同时取决于真实的物理流动特征和近壁面离散网格的空间布置。计算经验表明，若将μt修正为

则在局部网格加密控制的前提下，可以适当扩大低雷数求解的范围，利用SST湍流模型中ω方程对曲率变化的适应性和ε方程对来流涡频率的不敏感性特征，更好地求解梢涡精细流动。

分别采用上述修正SST模型和基于ω方程的雷诺应力模型（BSL-RSM）计算标准4叶桨E779A的梢涡流场特征如图4.1所示。该图中，分析工况为进速系数0.77，涡管同时以速度梯度的第二不变张量和旋转强度λci来可视化描述，其中，第二变张量表达式为

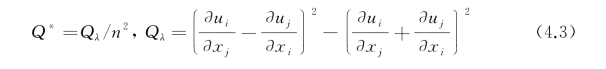
图4.1　E779A桨梢涡流动模拟

（a）修正SST湍流模型；（b）BSL RSM湍流模型；（c）修正SST模型模拟梢涡流动细节

式中，Qλ为涡量；n为转速；∂u/∂x为速度分量对坐标方向的偏导数。可以看出，来流、叶梢边界层流与由逆压梯度引起的二次流相互作用促使梢涡卷曲起始，形成梢涡流动，并且主涡涡束对梢涡涡核具有明显的包裹作用。此时，桨叶周围结构化离散网格与该桨用于水动力性能预报时的网格比较如图4.2所示，可见叶梢径向区域、周向螺旋区域和尾流轴向区域均进行了局部加密处理，以适应梢涡流动模拟。两种湍流模型求解的梢涡流动形态效果相当，因SST模型计算耗时明显少于RSM，后续推进泵梢涡流动模拟时仍首选修正SST湍流模型。

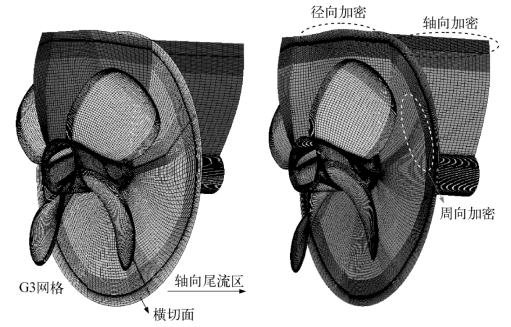
图4.2　E779A桨梢涡流动模拟时局部网格加密控制

其中，BSL-RSM湍流模型求解雷诺应力张量τij的表达式对应为

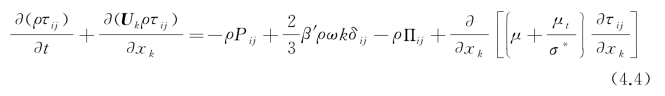
式中，i、j和k为坐标变量；Uk和xk分别为k方向速度分量和位置信息；δij为克罗狄克算子，当i=j时δij=1，否则为0。包含的ω输运方程为

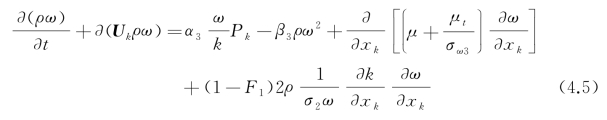
式中，Pk为黏性力诱导的流体湍动。与SST湍流模型一样，该模型也采用过渡函数使流动求解由基于ω的模型转变为基于ε的模型。在基于ω的模型求解时，参数取值为=2.0，σ1=2.0，β1=0.075，α1=0.553；基于ε的模型求解时，参数取值为=1.0，σ2=0.856，β2=0.082 8，α2=0.44。式（4.4）中压应力修正项表达式为

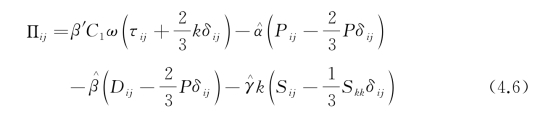
式中，雷诺应力源项对应为

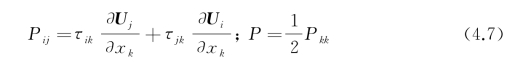
张量Dij表达式为

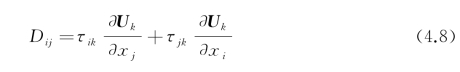
对应湍流黏度表达式为

(www.xing528.com)

与修正SST湍流模型中采用表达式相同，由此也间接证明了修正湍流模型的合理性。式（4.6）中参量取值为β′=0.09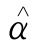，=（8+C2）/11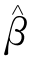，=（8C2-2）/11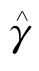，=（60C2-4）/55，C1=1.8，C2=0.52。

为了定量评估螺旋桨梢涡精细流场，再以水面舰艇常用母型桨DTMB5168为对象进行校验，美国海军水面战研究中心（Naval Surface Warfare Center Carderock Division，NSWCCD）公开了该桨敞水性能、空化初生性能曲线、尾流速度分布以及梢涡流场特征的众多试验数据，具有足够的信服力。该桨设计直径为402.7 mm，5叶，设计螺距下设计进速系数为1.27，梢涡流动测量主要针对进速系数1.1工况进行。

螺旋桨几何形状以及全结构化网格离散如图4.3所示。梢涡流动网格节点密度同时由沿桨叶径向方向、周向方向和轴向方向、桨叶壁面法向方向和叶截面弦长方向以及尾流轴向方向的节点进行控制。在桨叶导边区、随边区和叶梢区进行单独拓扑块关联并加密的基础上，为提高梢涡涡核运动轨迹的模拟精度，将桨叶0.8R叶截面以上径向空间均进行局部加密处理，一直到内旋转域径向分界面处为止。桨叶近壁面仍采用O形网格以提高网格正交性。计算时未考虑毂涡流动，直接采用贯穿轴来模拟。

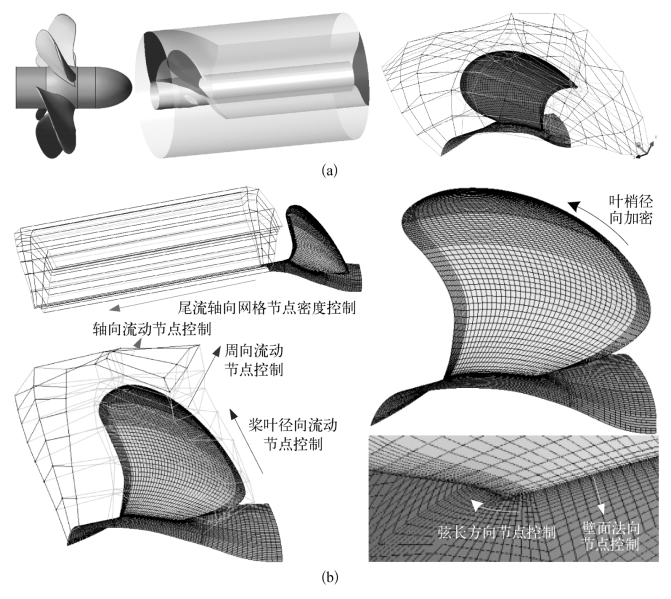
图4.3　DTMB5168桨几何形状、网格拓扑结构及壁面网格

（a）桨叶几何和网格拓扑结构；（b）梢涡流动区网格局部控制

计算时将桨叶缩小为标模直径250 mm，以将计算资源集中用于模拟梢涡流动特征。转速取20 r/s。计算得到螺旋桨敞水性能曲线与试验值比较如图4.4所示。除因几何尺度缩小使得推力和力矩系数略偏小外，在0.95～1.55进速系数区间内预报得到的推力和力矩系数均与试验值吻合较好。计算得到近尾流轴向横切面0.238 6R轴向、周向和径向速度分量以及湍流速度脉动量分布与试验值比较如图4.5所示。图4.5中，湍流速度脉动量与湍动能之间的对应关系为q=。可以看出，在进速系数J=1.1工况下，近尾流面的三个速度分量以及湍流速度脉动量均与试验值能吻合较好，特别是在叶梢径向位置能够定性模拟出梢涡的旋转特征。需要注意的是，图中速度分量（va，vt，vr）均对应为旋转坐标系中的变量，其与绝对坐标系中速度分量（ua，ut，ur）的对应关系为

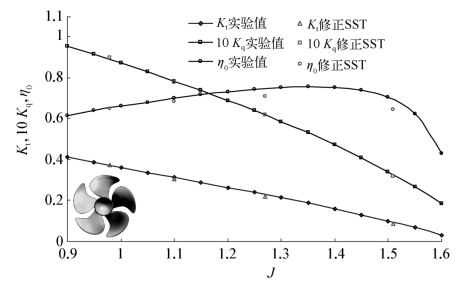
图4.4　DTMB5168桨敞水性能计算与校验

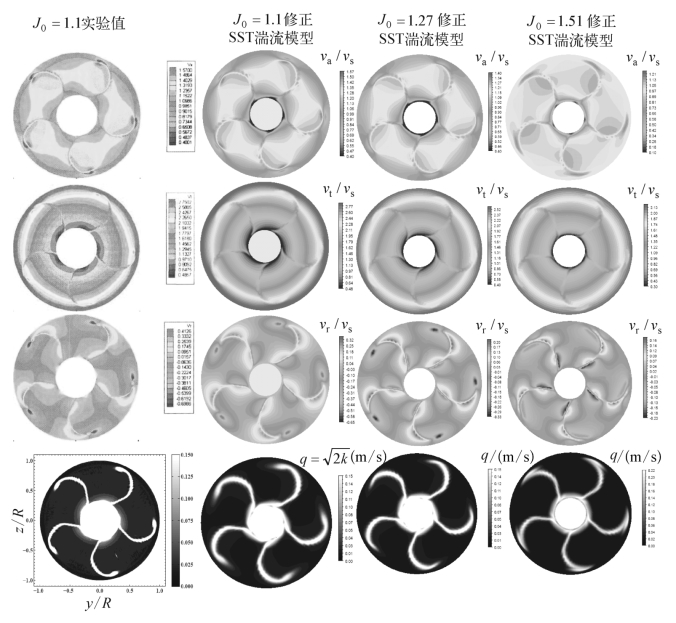
图4.5　螺旋桨近尾流速度分量与湍流速度脉动量预报

此时，该设计工况下桨叶梢涡流管形态以及涡核湍流速度脉动量分布如图4.6所示，与前述4叶桨有一定的相似性。

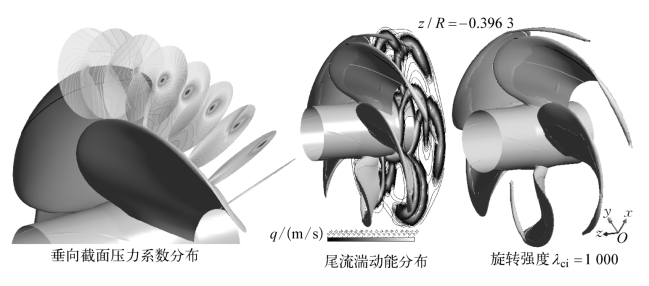
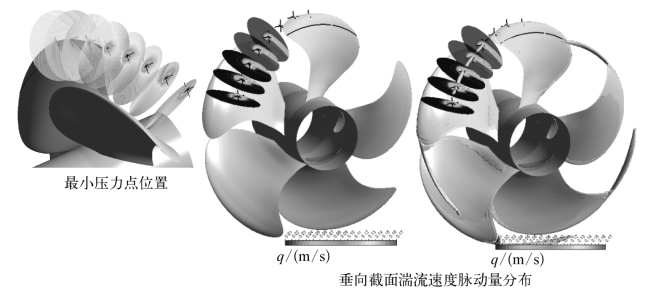
图4.6　螺旋桨梢涡运动轨迹、涡核压力和湍动能分布

计算得到该横切面上周向平均速度分量沿径向分布如图4.7所示。可以看出，四种进速系数工况下，不同半径处轴向和周向速度分量均与试验值吻合很好，径向速度分量在0.9R叶截面以下部位与试验值之间存在较明显的偏差。计算得到该平面上0.7R和0.92R径向位置处的速度分量沿周向分布如图4.8所示。图中同时给出了两个径向位置处的试验值，但因无法得知测点布置周向角度，所以未迭加在一起进行比较。可知，速度分量沿周向变化特征能够与试验值吻合。两个径向位置处周向速度和径向速度分量的峰值均较试验值略小，存在一定的偏差。计算得到的涡核中心距旋转轴距离随轴向位置变化与试验值比较如图4.9所示。可以看出，在尾流轴向0.3R距离以内，计算得到的涡核中心与试验值吻合较好。但随着向下游方向移动，因网格节点数量的总体控制要求，在轴向方向上网格逐渐稀化，使得预报涡核的径向距离较试验值稍大。

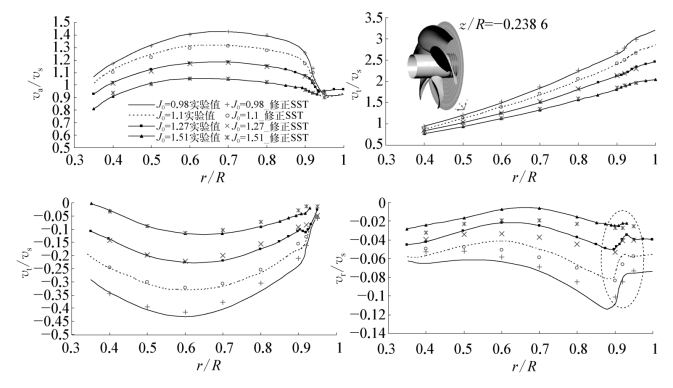
图4.7　螺旋桨近尾流周向平均速度分量

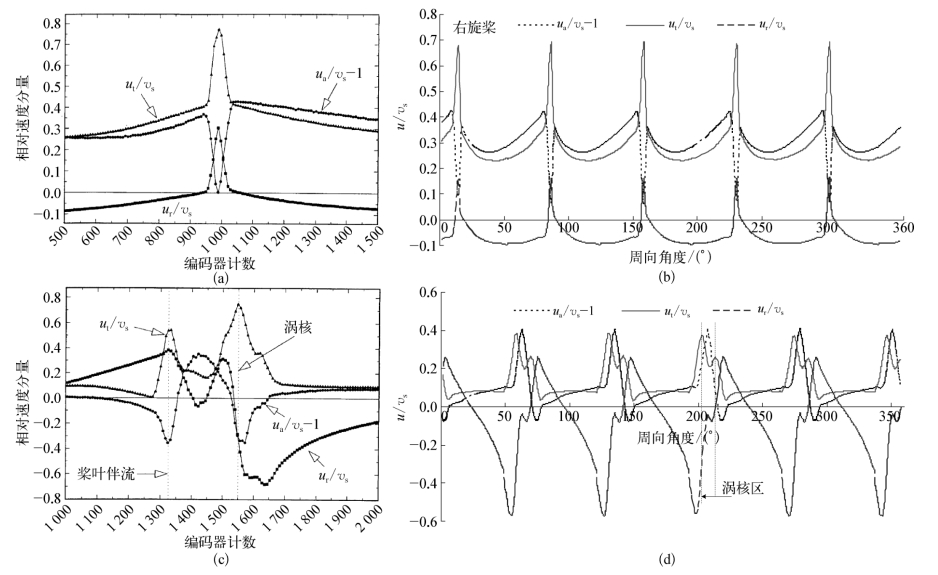
图4.8　螺旋桨近尾流面速度分量随周向位置变化规律

（a）左旋桨，z=-0.2386R，r=0.7R＿实验值；（b）右旋桨，z=-0.2386R，r=0.7R＿计算值；（c）左旋桨，z=-0.2386R，r=0.92R＿实验值；（d）右旋桨，z=-0.2386R，r=0.92R＿计算值

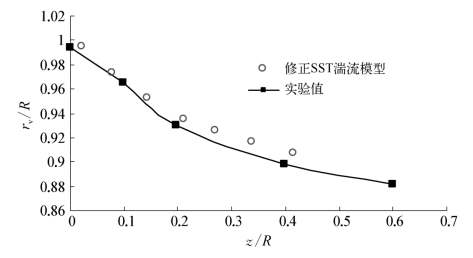
图4.9　螺旋桨梢涡涡核运动轨迹

由上述定量比较校验可知，所采用的修正SST湍流模型以及所建立的梢涡流场数值模型对于螺旋桨梢涡精细流动模拟来说是适用的、可信的，可以进一步用于推进泵叶梢间隙流场的数值模拟与分析。