为真实检验上述进水流道参数化设计方法的工程实用性,首先以美国海军水面战研究中心委托交通运输部(Center for the Commercial Development of Transportation Technologies,CCDo TT)为其高速瘦长型运输补给船Sealift特制研发的先进轴流外型混流式喷泵系统为例进行对比分析。该船设计航速为50 kn,泵进口直径为2 286 mm、喷口直径为1 483.36 mm,单泵额定功率为57 330 hp、额定转速为406.9 r/min、泵流量为68.128 m3/s、扬程为56.144 m,泵吸口比转速为15 005(美制单位)。该泵匹配的进水流道轴面曲线和三维几何形状如图3.26所示,由图示数据可知,流道出口的相对安装高度Dh/D不大于0.7,流道总相对长度L/D约为3.75,流道倾角未知。流道下壁面无直管段,与前述设计结论一致。
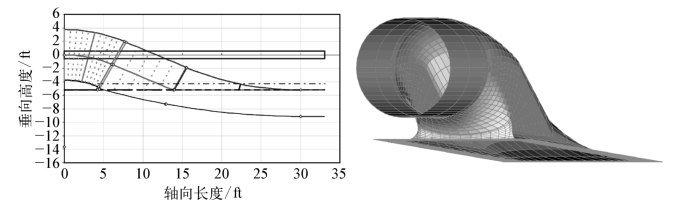
图3.26 高速喷泵系统平进口式进水流道轴面曲线和三维几何形状
根据前述分析,取流道出口相对高度Dh/D=0.7、流道倾角αD=23°,设计下壁面无直管段的归一化进水流道,包括弯管段、上壁面直管段、背部圆弧区域、唇部以及进口截面曲线。流道出口直径为单位尺寸1 m,取唇部半径R4/D=3.5%。由式(3.24)可得弯管半径R1/D=2.670 3,由坐标点表达式可得中轴曲线端点X5/D=2.090 7,由式(3.25)可得背部圆弧段半径式R5/D=5.789 7,由式(3.26)可得流道总长L/D=4.548 2,由式(3.28)可得流道进口截面长度Lin/D=3.859。在确定控制点A1~A17的坐标值后,可确定二维轴面曲线型线。进口截面取为方形与椭圆形的组合,即长度系数k1=k2=1。在生成上壁面两条辅助曲线和一组截面型线后,即可得到该进水流道的三维几何参数。
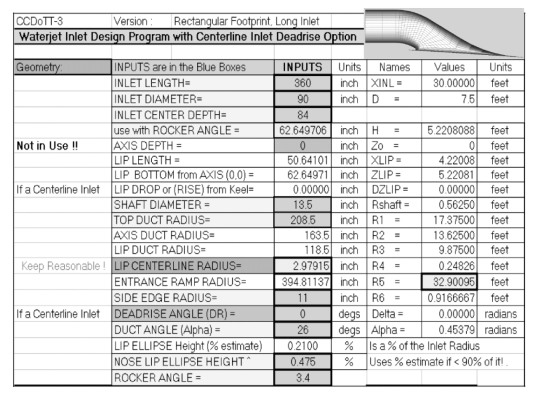
将流道总长、出口高度、唇部长度、弯管上壁面半径、唇部半径以及背部圆弧半径等关键参数值与CCDo TT发布的进水流道设计报告中取值(见图3.27)进行比较,分析两者之间的偏差,比较结果如表3.1所示。可知除背部圆弧半径偏小约5%外,其余总体参数之间的偏差均小于4%。此外,课题组还找到了该机构为该船所设计的短流道方案,方案显示流道倾角增加、流道总长减小、船尾上扬角3.4°,并且设计方案明确表述了考虑船尾上扬角时出口高度应减小,如图3.28所示,再次用于定量校核本设计方法。结果显示,流道总长与弯管半径这两个关键参数的偏差均小于1%,且除了唇部长度偏差约5%外,其余设计参量的偏差均控制在2%以内,由此表明本设计方法完全适用于中高航速下泵推系统进水流道的设计要求。更重要的是,无论是长流道还是短流道,CCDo TT在完成流道设计时都采用了流道总长L、流道出口直径D、弯管上壁面半径R1、出口中心高度Dh和流道倾角αD5个全局控制参数,并且这5个全局参数相互之间并未表现出相关联系,新流道设计时无法直接借鉴参考。本设计方法基于流道倾角这一单一控制参数来完成整个参数化设计,在方法和可操作性上有着显著改进,具有明显的工程实用价值。
表3.1 两种方法设计某高速喷泵进水流道关键几何参数比较
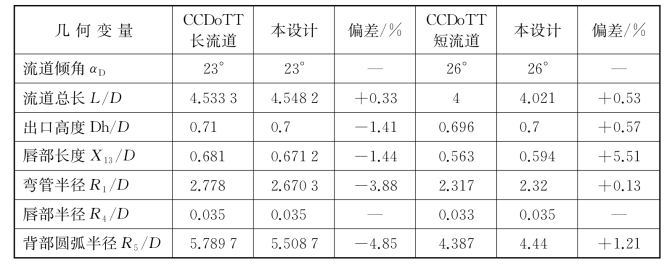
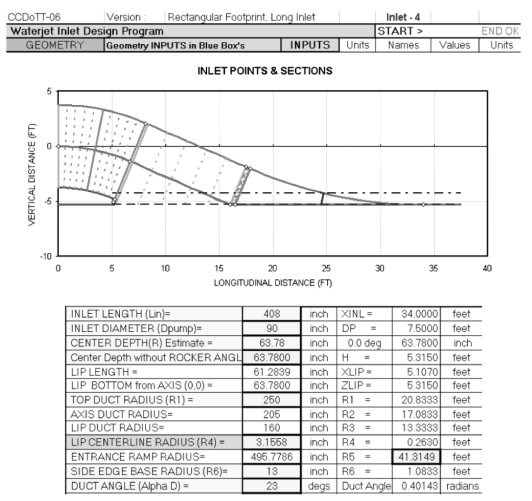
图3.27 CCDoTT设计的某高速喷泵系统平进口式长进水流道
 (https://www.xing528.com)
(https://www.xing528.com)
图3.28 CCDoTT设计的某高速喷泵系统平进口式短进水流道
此外,为了充分检验本设计方法的有效性,再次针对国际一流喷泵推进厂商MJP公司的MJP750流道(出口直径750 mm)进行设计检验。该流道下壁面拥有直管段。保持流道倾角23°和出口中心相对高度1.227与原设计一致,取下壁面无直管段时母型流道的出口中心相对高度为0.65,参数化设计得到流道关键几何参数与原流道几何值(型值测量)的比较如表3.2所示。可知,除流道总长更短、唇部下缘更长(两者均偏差约20%)外,弯管上壁面半径偏差小于6%、下壁面和上壁面的直管段长度均偏差小于1%,非常贴近于原流道几何参数。流道总长和唇部下缘长度出现较为明显偏差的原因是,原几何形状背部区域和唇部区域均采用三阶贝塞尔曲线,并没有采用圆弧方案,且均由两个形状参数来控制其型值,如图3.29所示,使得轴面曲线图中的进口切点A9右移、唇部下缘端点A12左移,进而与本设计采用圆弧方案出现了较大偏差。该变化对流道性能的影响主要体现在影响进口截面进流,进而影响进口能量损失系数,属于局部参数优化,在方案设计阶段可以将其与流道几何参数设计解耦。注意,该图中L1直管段是在弯管段的下游方向水平延伸的一段直管,便于进行流道试验测量。由上述比较分析可知,本设计提出的基于流道倾角单一几何参数控制来完成进水流道参数化设计同样满足“出口安装高度较高、流道下壁面需增加直管段”的应用需求,结合前述下壁面无直管段时的应用检验,很好地证明了本设计方法的工程适用性。至于“出口安装高度带来的流道下壁面是否需要增加直管段以及直管段最小长度”与设计航速之间的关联机制,或者说同一流道倾角时下壁面增加直管段前后所最优适应的航速区间是否有所变化,还需要系列化分析流道的流体动力性能。
表3.2 本方法设计某高速喷泵进水流道关键几何参数与原厂几何参数比较
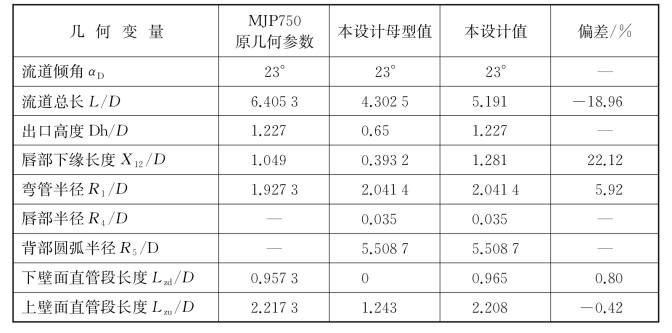
图3.29 MJP750进水流道轴面曲线
最后,既然该参数化设计方法同时适用于艉板安装的长流道、短流道、高流道和矮流道设计,完全可以称之为基于单一几何参数控制的通用化流道设计,那么,能否适用于浸没式喷泵的进水流道设计呢?仔细观察美军试验用AWJ-21浸没式喷泵,可知,一方面存在喷口下倾角,且该下倾角等于轴系倾角;另一方面流道下壁面不仅没有直管段,而且流道出口的高度几乎减小至极限,如相对安装高度取值0.6,甚至更小。结合上节分析可知,无论是否考虑船尾上扬角影响,前文得出的轴面投影曲线建立方法同样适用于浸没式流道设计。那么,最后的问题就转化为了如何来确定相对最优的进口截面。再次参照AWJ-21的流道截面图,一方面可以看出流道倾角较小,甚至可能不足20°;另一方面流道进口截面已经由常见的平进口式变为了内凹的复杂曲面,以保证未流入进水流道的流体能够顺畅地流向船尾下游,减小流动阻塞。在尚未进行流动性能校核的条件下,可初步选取如图3.5所示轴面投影图中的A5A8中点为特征点Ac,相当于为流道的轴面投影曲线增加两段圆弧,一段为过Ac和A9点且与水平面相切,另一段为过A12和Ac点且与前一段圆弧外切,如图3.30所示,在保持进口截面四周边缘曲线同样为方形与半椭圆组合曲线不变的情况下,即可精确确定内凹式进口截面的三维曲面,由此完成了基于单一几何参数控制的浸没式喷泵进水流道参数化设计,证明了本设计方法的通用性价值。
图3.30 浸没式喷泵进水流道的参数化设计
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




