尽管已经由上述几个全局控制参数完成了平进口式进水流道二维轴面曲线的几何参数化设计,但几个全局控制参数之间的相互约束机制还不明确,配合取值是否合理,或者说配合取值后实现的进水流道的性能是否优秀还不清楚。并且,在给定船尾总体安装尺寸限制的情况下,如何来取到一组相对最优的参数值,以适应泵的推进单元设计,或者说在方案设计阶段就完成泵推系统总推进效率的评估,仅凭这样一组全局控制参数在几何上进行试凑约束显然是无法实现的。为此,还需要进一步精简全局控制参数,并且从流道小型化和轻型化设计的角度明确控制参数的实用取值范围,以增强进水流道几何参数化设计的可操作性和实用性。
为了合理选取相对较少的关键几何控制参数,需要将几何约束与性能表现结合起来衡量。KaMeWa公司的设计经验表明,变量进速比IVR(航速与流道出口平均速度的比值)可以综合反应喷泵进水流道内的流动状态。当航速相对较低时,IVR小于1,流道进口处虚拟流管分界面的驻点位于唇部外侧,将导致唇部内侧区域出现流动分离甚至产生空化(见图3.6);当泵类推进系统在设计航速工作时,典型喷泵的进水流道IVR介于1.3~1.8。与低速流道相比,流道内的流动状态发生显著改变,特别是当IVR大于1.5时,流道出口速度明显小于航速,意味着管道内流体存在明显的减速作用。此时,虚拟流管分界面的驻点将上移至唇部内侧(见图3.7),一方面,唇部外侧区域因为流体的局部加速有可能产生空化;另一方面,管道内逆压梯度的存在将使得上壁面背部区域发生较为明显的流动分离,均对系统总推进效率和抗空化性能不利。可以说,应用需求的差异直接决定了流道几何参数的差异。从外形上看,高航速进水流道的流道倾角更小,流道总长相对更长;而低航速进水流道在直管段更陡,总体更短,以适应进流大角度吸入的基本特征。需要注意的是,鉴于喷水推进船能够快速、便捷地实现低航速到高航速之间的切换,甚至在设计转速下也可以方便地实现零航速驻航,使得进水流道设计必须要尽可能兼顾设计航速和低航速需求,尽可能扩大其无空化和流动分离的航速工作区间,以最优化其流动性能。

图3.6 低航速进水流道内流动状态
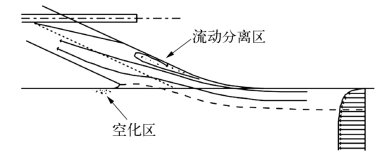
图3.7 高航速进水流道内流动状态
从上述设计经验可知,航速需求总体上决定了流道倾角的选取范围,航速越高,倾角越小,反之,航速越低,倾角越大;同时,倾角范围也总体限制了流道总长,小倾角流道相对更为紧凑,总长更小;流道唇部半径不能太小,要同时适应低航速和高航速推进应用的流道更是如此。因唇部半径由弯管半径、出口高度和倾角三者共同决定,在暂不考虑背部圆弧段几何参数的条件下,流道倾角既能直接影响另外两个全局参数(弯管半径R1和出口高度Dh,其出口直径D已知)的取值,又与流道的流动性能密切相关,正是关键几何控制参数的理想选择。
基于此,首先将泵进口直径归一化为单位直径1 m,然后取消唇部半径R4和背部圆弧段半径R5参数,再将弯管半径R1和流道出口高度Dh转换为相对尺寸R1/D和Dh/D,最后由流道倾角来全局控制二维流道的轴面曲线,看能否实现归一化流道的单一参数化设计。归一化流道的轴面曲线坐标点定义与图3.5中一致,简化后轴面曲线仅由A1、A2、A3、A5、A6、A9和A107个点决定,如图3.8所示。
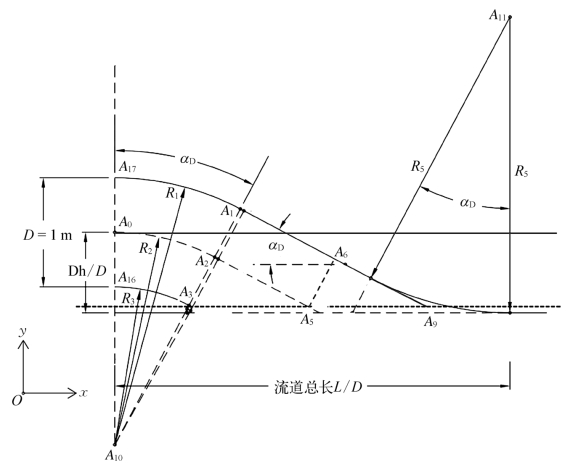
图3.8 简化平进口式进水流道二维轴面曲线
令式(3.18)中R4=0,可得R1/D随倾角的变化关系式为

可知,当出口高度已知时,弯管半径由流道倾角唯一决定。出口高度越小,流道的位能抬升能量损失越小。依据常见安装尺寸限制和设计经验,当采用混流泵推进时,泵安装法兰的根部直径通常为泵进口直径的1.4倍(见图3.9),则出口高度的最小取值为(Dh/D)min=0.7;若采用轴流泵推进,出口高度的最小取值可以进一步减小为(Dh/D)min=0.6。由此,可将Dh/D的优选取值固化为0.7,当安装尺寸较为宽松时,可适当将该值放大至0.85甚至是1.0。再次根据几何参数代数关系得到特征点的坐标值如下:

图3.9 典型喷泵安装尺寸
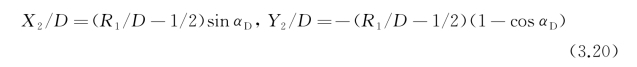
![]() (https://www.xing528.com)
(https://www.xing528.com)
![]()
![]()
式(3.23)中,X9即为简化流道总长Lj。由上述表达式可知,特征点A2、A5、A6、A9和A10均由流道倾角唯一确定,至此实现了简化平进口式归一化流道的单一几何参数控制。
为了增强流道参数化设计的工程实用性,先将唇部半径R4/D还原,仍然取消背部圆弧半径R5/D,则此时唇部半径和弯管半径表达式分别为

可知,当流道出口高度确定后,无论是弯管半径还是唇部半径,均由流道倾角唯一确定,与是否存在唇部无关。并且,轴面曲线的特征点A2、A5、A6、A9和A10的坐标值与简化流道完全相同,不因增加唇部而改变。至此,只需还原背部圆弧几何形状,并且实现背部圆弧半径R5/D由倾角确定,即可完成真实平进口式进水流道基于单一几何参数控制的参数化设计,并且能够总体保证流道的品质效能。
再次分析如图3.5和图3.8所示的轴面曲线,根据外圆相切性质,可得背部圆弧半径的表达式为
![]()
则真实流道总长L相对于简化流道总长Lj所增加的长度为ΔL=0.5/tanαD,最终流道总长随倾角的单一变化关系式为
![]()
该式表明,背部圆弧切点A9和中轴曲线水平交点A5之间的距离与出口直径的比值为0.5(1/sinαD+1/tanαD),仅随流道倾角变化,而与流道出口中心高度无关。再结合唇部水平切点A12(见图3.5)和点A5之间的距离与出口直径的比值

可得进水流道进口截面长度Lin表达式为
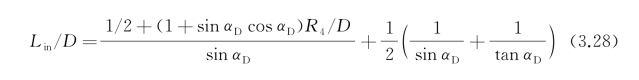
至此,依据工程设计经验给定流道出口高度值后,弯管段上壁面半径、唇部半径、背部圆弧段半径、流道总长和流道进口长度均由流道倾角唯一确定,完成了平进口式归一化流道(出口直径为1 m)基于单一几何参数控制的轴面曲线参数化设计工作。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




