泵类推进器振动和噪声控制机理

即使考虑能量损失，泵效率也仅仅是单个部件的性能，在独立性上与桨敞水效率类似。当泵与管道系统匹配时，或者是推进泵与进水流道及船体边界层流匹配时，泵的运转性能显然会较大地偏离理想工作条件，既要保证工作点不能偏离最佳效率点（best efficiency point，BEP）太远，还要保证泵能够自吸、能够正常地运送流体、具有克服流体汽化所需的最小能量头以及较大的安全工作裕度。这些性能需求将泵从一个部件扩展到了整个流动系统，也给泵性能的试验评估提出了原则性的要求。比如，模型尺度泵和实尺泵之间必须同时满足几何条件相似、流动相似和动力学相似，最后才能保证性能相似，才能进行性能曲线的相似转换，与模型桨敞水性能试验时换算方法类似。

依据布金汉π定理，以来流速度、转速和直径为基本特征参数，定义4个量纲一的参数——进速系数J、空化数σ、雷诺数Re（基于转速参量）和傅汝德数Fr后，可通过模型试验测量模型桨的推力系数和力矩系数，并依据相似关系换算得到实尺桨的推力系数和力矩系数。量纲一的参数表达式为

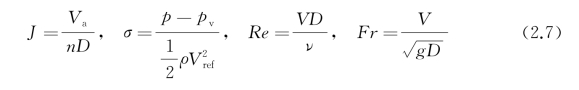
式中，p为流场局部压力；pv为汽化压力；Vref为参考速度，可以是来流速度，也可以是叶梢线速度；V为来流速度；ν为运动黏度。显然，在实际应用中，模型与实尺同时满足四个量纲一的参数相等是不可能的，特别是雷诺数和傅汝德数难以同时满足。因此，在几何条件相似的前提下，首先要保证进速系数相等，使桨的工作点不变；其次，因空化对流体流动和受力均影响显著，故需要保持空化数相等；最后，测量表明当雷诺数高于临界雷诺数时，可以忽略傅汝德数不相等带来的影响。所以，当前在模型桨敞水性能试验测量实施时，通常采用的量纲一的相似参数为式中，σn为基于叶梢线速度的空化数；c0.7R为0.7R叶截面弦长；Re0.7R为0.7R叶截面处合速度对应的雷诺数。在上述三个相似参数的控制下，一方面认为几何相似的不同尺度桨其敞水性能曲线以及空化性能相同，另一方面，依据工作点不变可以调整推进系统中航速和转速的匹配，如车令表中正常工作制的制订。从理论上讲，泵与桨都是旋转叶片机械，上述相似应用可以直接类推到推进泵的分析中。但是，因为流体流动从以外流为主转变为以内流为主，基本特征参数将发生变化，尚不能直接全盘应用。

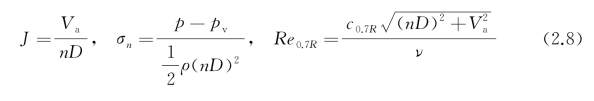
再次应用布金汉π定理，并且以密度、转速和直径作为基本特征参数，可以得到5个量纲一的参数，分别对应为比流量、比扬程、比功率、雷诺数和相对粗糙度，表达式为

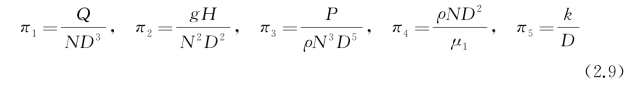
式中，N为转速，单位为r/min；Q为体积流量，单位为m3/s；D为泵进口直径，单位为m；H为扬程，单位为m；P为功率，单位为W；μ1为动力黏度，单位为N·s/m2；k为粗糙度，单位为m。与螺旋桨类同，模型泵与实尺泵雷诺数相等也难以满足，而且由于雷诺数正比于直径的平方，偏差量比Re0.7R更大，表现出来的尺度效应对性能曲线的影响也更大，这也是通常实尺泵比模型泵效率高2%～4%的原因所在。相对粗糙度一般由加工精度给予保证，相似换算时暂不考虑。5个量纲一的参数中并未包含空化数，原因是泵作为组合式推进器，其空化产生、发展以及对性能的影响更加复杂，而且与泵和系统的抗空化性能同时相关，因此通常给予单独分析讨论。同样，在实际工程应用中，在几何参数相似的基础上，当比流量、比扬程和比功率分别相等时，模型泵与实尺泵之间满足动力学相似，从而可以进行相似换算。

那么，随之而来的问题是，选型设计时如何来判断是否满足几何参数相似呢？特别是在当前国内成功的推进泵样本非常少的情况下，是否能仅凭几何尺寸和泵功率等级进行判断？如果不能，不熟悉泵产品的设计师又该如何选择最为合适的推进泵？

针对这些问题，将比流量和比扬程量纲一的参数经过变化后统一起来，重新引入一个量纲一的参数，以便在不考虑泵几何尺寸的条件下将泵过流能力与做功能力同时界定，达到直接通过性能来选用泵的目的，这就是比转速，其定义式为显然，比转速是一个形状参数，是可以直接衡量泵几何参数相似的量纲一的参数。需要注意的是，因为推进泵的应用是从水利泵过渡而来，加上当前普及推进泵应用的主要是欧美海军，使得比转速在不同使用习惯驱使下，无论是变量形式还是单位组合都有较大的差异，导致具体数值相差巨大，进而使得相关公开文献中的技术与试验数据必须经过转换处理后才能应用，给选型设计的有效实施增添了障碍。为了解决这一问题，将典型比转速nω的变量表达式、单位以及换算系数陈述如下：

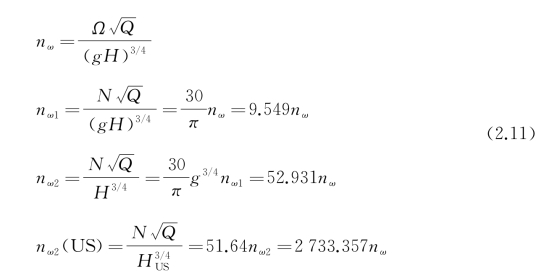
式中，Q的单位为m3/s；Ω的单位为r/s；H的单位为m；HUS的单位为ft（英尺，1 ft=3.048×10-1m）；N的单位为r/min。其中，课题组常用表达式nω与经典泵教材Hydrodynamics of Pumps［10］是统一的。选型设计时，根据比转速值，不仅可以确定泵类型，而且可以直接定位泵产品几何，甚至还可以将其与性能参数直接关联起来，如效率和功率密度，可供推进泵选用与设计直接参考。不过，实际应用该参数时，还需要注意不同单位给出的推荐值有所不同，如专著《泵喷推进器的低噪声设计机理与设计应用》中推荐的“当1.46＜nω＜3.66时为混流泵，nω＞3.66时为轴流泵”，文献［11］中推荐的“5 000＜nω2（US）＜10 000时为混流泵，10 000＜nω2（US）＜15 000时为轴流泵”，以及Ka MeWa公司推荐的“通常nω＞3.4时认为是轴流泵，1.0＜nω＜3.4时为混流泵，且高质量的喷泵比转速nω2（US）约为8 000”。课题组常用的泵效率随比转速的变化规律曲线如图2.9所示，代表了2005年来推进泵的设计水平，选型设计时可根据该图查找比转速后直接给定泵效率初始值。从比转速的表达式可知，当扬程和流量一定时，比转速增加意味着泵转速增加，功率一定时相当于力矩减小，从而可以在一定程度上减小体积和重量，这对于水下航行器以及中小型船舶等特别关注轻型化设计的泵类推进系统选型设计来说，是一个顶层设计问题，尤其需要关注。(www.xing528.com)

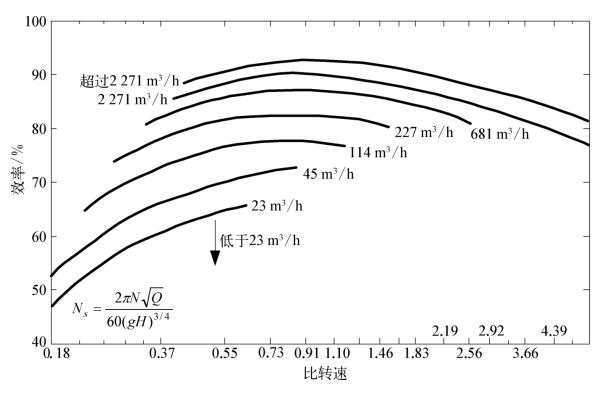
图2.9　泵效率随比转速的变化规律经验取值

解决了选泵的问题后，接下来需要考虑的问题是，泵厂商通常发布的泵性能曲线默认为工作于额定转速，但选型设计时往往考核点并不在设计点上，或者说除了设计航速外，其他考核点的性能曲线同样受到关注，如巡航航速。那么，如何才能实现像螺旋桨一样通过控制工作点不变来保持航速与转速的匹配，进而使得推进器始终位于高效区呢？尽管比流量参数有点类似于螺旋桨进速系数，根据比流量不变，可以得出转速改变后的对应流量，但仅靠该参数还难以得出变工况后的扬程和功率值，还需要借助其他参量。

为了满足这一需求，利用前述定义的量纲一的参数，重新引入三个常用系数，即流量系数、扬程系数和功率系数，以定量控制泵的工作点，并且功率系数可以由流量系数和扬程系数推导得出，然后将泵性能曲线表述为扬程系数、功率系数和效率分别随流量系数的变化关系，进而可以直接类比于螺旋桨敞水性能曲线图中的推力系数、力矩系数和敞水效率，以实现泵和桨两者同样作为推进器的统一。其中，流量系数φ、扬程系数ψ和功率系数P*的表达式分别为

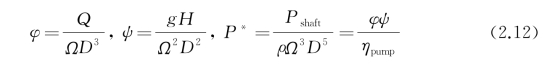
式中，Q为流量，单位为m3/s；Ω为角速度，单位为rad/s；H为扬程，单位为m；D为直径，单位为m；Pshaft为轴功率，单位为W。图2.8中典型推进泵的量纲一的性能曲线如图2.10所示。注意，该图中量纲一的系数的定义式与式（2.12）略有不同。可以看出，流量系数φ就相当于螺旋桨进速系数J，直接控制泵的工作点。当工作点改变后，可以直接读取扬程系数、功率系数和效率，进而根据转速的变化求取新的流量、扬程、功率和效率值，实现多工况下泵类推进系统性能参数的选型设计。并且，当保持工作点不变时，如同车令表中工作制的制订，可以直接得出：泵流量正比于转速，扬程正比于转速的平方，功率正比于转速的三次方。显然，当流量系数和扬程系数均保持不变时，比转速同样保持不变。这也正是Ka MeWa公司在展示其同一系列、不同进口直径的喷泵产品时，直接表述为P=C（N/1 000）3的原因所在。式中，N为转速，单位为r/min；C为功率系数，意为转速1 000 r/min时喷泵所吸收的功率，单位为kW，该值可由测量或者数值计算得到的不同尺寸喷泵的功率-转速曲线求取，如图2.11中所示。

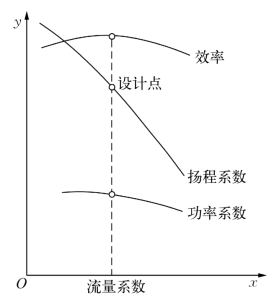
图2.10　某推进泵扬程系数、功率系数和效率随流量系数的变化曲线

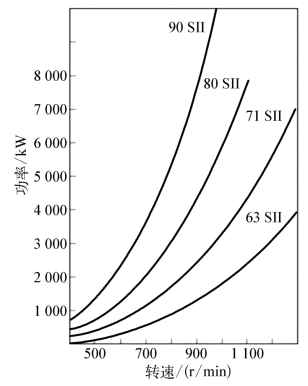
图2.11　KaMeWa公司SII系列、不同进口直径的喷泵功率随转速变化曲线

综上所述，泵类推进系统选型设计时，以比转速作为泵几何相似的衡量参数，确定泵类型的同时直接定位母型泵产品；引入流量系数、扬程系数和功率系数三个量纲一的系数后，将扬程系数、功率系数和泵效率随流量系数的变化曲线作为泵的量纲一的性能曲线，类同于螺旋桨敞水性能曲线，既可以描述不同尺度但几何参数相似的泵的性能参数，也可以描述相同泵在转速变化后的性能曲线；流量系数类比于螺旋桨进速系数，直接控制泵工作点；当转速改变但保持工作点不变时，流量正比于转速，扬程正比于转速的平方，功率正比于转速的三次方，由此可以实现新的运转参数配合，但泵依然工作于高效点，可以用于泵类推进系统车令表的制订。