泵类推进器振动和噪声控制机理的基本原理和应用

泵类推进系统的核心部件是推进泵单元。显然，它首先是一个泵，然后才是一个推进泵。因此，阐述清楚泵的基本理论对于不太熟悉叶轮机械的螺旋桨设计人员来说，将有利于加深其对螺旋桨和推进泵的内在联系以及主要差异的理解，以更好地牵引和指导选型设计工作。

对泵的认识可以从“泵是如何工作的”“不同类型泵之间有何显著差异”两方面入手。显然，这两个问题的答案直接服务于泵的典型性能需求：一是泵与管道系统之间如何匹配，即给定管道系统后，如何选配最合适的泵尺寸和类型；二是泵内流体流动具有的能量究竟如何转换，如何衡量能量转换的效率；三是如何来量化决定泵的需求功率。这三个问题既是一般水力机械泵所关注的理论设计问题，也是推进泵同样需要阐述清楚的焦点性问题。

泵内流体在流经叶栅通道的过程中获得能量，而表述流体能量头与转子运转之间内在联系的经典理论为欧拉方程，即单位质量的流体所获得的能量头（扬程）为

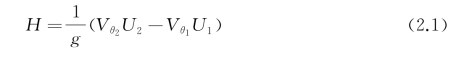
式中，Vθ2和Vθ1分别为流体在转子（叶轮）出口与进口的绝对速度周向分量；U2和U1分别为转子（叶轮）出口与进口的圆周速度。显然，泵内流体在获得能量的过程中所消耗的功率为ρgQH，其中Q为体积流量。在已知泵对流体做功的过程中实际消耗的功率P后，即可得到泵的水力效率，一般简称泵效率ηpump，则有

泵效率与泵类型、尺寸、运转参数以及工作点有关，通常所说的泵效率特指设计工况下的效率，类似于螺旋桨敞水效率通常指最高点或者是近最高点效率。敞水效率的定义式为

式中，Va为均匀来流条件下螺旋桨轴向进速；T为螺旋桨轴向推力；Qp为消耗力矩；下标0代表敞水条件（均匀来流）；n为转速，单位为r/s；J为表征螺旋桨工作点的进速系数；KT和KQ分别为推力系数和力矩系数，定义式为

式中，D为螺旋桨直径。显然，敞水效率表征的是均匀来流条件下螺旋桨轴向推力做功的能力，是轴向利用推进能量的效率。泵效率不同于敞水效率，其表述的是泵转子对泵内流体做功时总的能量转换效率，测量时通常也为均匀进流条件。但是，泵内流体所具有的能量并非全在轴向，也并非所有有效能量都能用于轴向推进。泵效率通常较高（现代泵效率一般为0.85～0.92［9］），主要用于衡量转子（叶轮）叶片控制通道内流体能量损失的能力，并未与轴向推力直接联系起来。

常见的泵类型有离心泵、混流泵和轴流泵，三者在几何上差异明显，容易区分，如图2.5中泵转子（叶轮）的轴面投影图所示。图中r1、r2分别为进、出口半径。当出流与轴向夹角θ呈90°时为离心泵，平行于轴向时为轴流泵，0°＜θ＜90°时为混流泵。定性上看，离心泵具有大扬程、小流量的特点，而轴流泵具有大流量、小扬程的特点，其内部流动形式类似于管内螺旋桨。混流泵的扬程和流量均介于两者之间，理论可达的高效区相对最广。正因如此，喷泵多采用混流泵和轴流泵，而泵喷更多采用的是轴流泵。如果仅从几何外形和性能特点上来区分不同类型泵，是较为清晰、明确的，但泵类推进系统选型设计时往往较难以实施，若设计人员缺乏经验则更难以着手。原因在于，一方面，当前水利机械行业领域内用于区分混流泵和轴流泵的特征参数临界点并不十分明确，不同设计单位取值也不相同，当作为推进泵应用时，其临界值更是还没有统一结论；另一方面，选型设计时，泵的运转参数和工作点均具有较大变化范围，如果不能将作为部件的泵的性能融入泵类推进系统性能中进行综合寻优，往往将无法挑选出最为合适的泵类型，使得选型设计在大方向上偏离真值较远，给设计工作带来极大的困难。因此，有必要从性能曲线的角度来定量描述典型泵的性能特点，以加深理解。

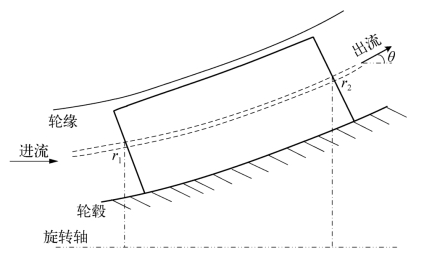
图2.5　泵转子（叶轮）轴面投影(www.xing528.com)

螺旋桨敞水性能曲线表征的是均匀来流条件下螺旋桨轴向推力和消耗力矩随工作点的变化关系，典型螺旋桨敞水性能曲线如图2.6所示。因力矩系数值较小，放大10倍后取值。可见，螺旋桨桨叶几何参数确定后（螺距不变），敞水性能唯一确定；工作点改变时仅具有单一高效点，且高效区很窄。

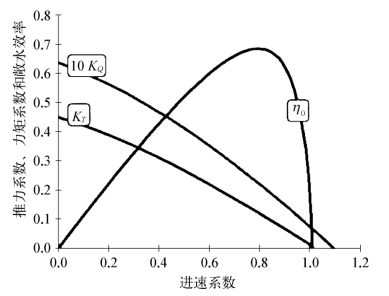
图2.6　典型螺旋桨敞水性能曲线

类同于螺旋桨敞水性能曲线唯一由螺旋桨几何参数确定，泵转子（叶轮）与定子（导叶）叶型确定后，其性能曲线同样唯一地确定。如果能够建立叶型几何参数与性能参数之间的直接联系，则泵性能曲线可以定量再现叶型对流体的做功能力，从而反过来指导叶型设计。参照螺旋桨叶截面受力分析时速度三角形的分解思路，取转子（叶轮）叶片半径r处的叶截面进行分析，如图2.7所示。定义流动角β（r）为轴面图中相对速度与垂直于轴向的横截面之间的夹角，下标1和2分别代表进流与出流；叶片安放角βb（r）为轴面图中叶截面拱线切线方向与垂直于轴向的横截面之间的夹角，由叶片几何决定，与螺旋桨叶截面分析时螺距角对应；入射角α（r）为叶片安放角与进流角之间的差值，即

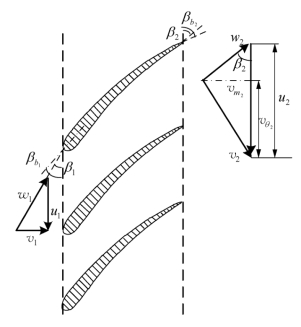
图2.7　转子（叶轮）叶截面进出口　特征角与速度三角形

入射角与螺旋桨叶截面分析时攻角对应。v、u和w分别为绝对速度、牵连速度和相对速度；vm和vθ分别为轴面速度分量和周向速度分量。理论分析和设计时通常假定转子进流仅有轴向速度分量，即tanβ1（r）=v1（r）/r1Ω，Ω为转子角速度。当流量和转速已知时，进流角即可确定，从而可直接确定入射角，并可借助翼型升阻力曲线来分析叶截面受力。同时，当转子轴面投影进一步特殊化为轴流通道时，式（2.1）可转化为

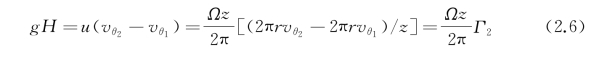
式中，z为叶片数；Γ为环量。可以看出，转子叶型做功能力由叶片出口的环量分布唯一确定。再根据翼型升力定理，可知转子叶片受力同样由叶片出口环量分布确定。这既将叶片几何与性能参数联系起来，也是后文转子叶型由性能到几何的参数化三元逆向设计的基础所在。若将轴面几何投影还原为混流式通道，则式（2.6）右边的流体获得能量项中应增加径向方向能量，变为g H=+（Ωz/2π）Γ2，物理意义不变。

根据出口速度三角形分解可得和，与式（2.6）联立且假定进口周向速度分量为零，可得H=a N2+b NQcQ2，式中，N为泵转速，单位为r/min；Q为体积流量，单位为m3/s；a、b和c为转子几何形状决定的常系数。可知：当转速一定时，转子扬程随流量增加而呈二次方减小，这也是泵行业中熟知的理想HQ曲线，显然，理想P-Q曲线表现为功率随流量增加呈三次方非线性减小。当考虑泵内流动能量损失后，典型推进泵在转速一定时，其扬程、功率和效率随流量的变化曲线如图2.8所示，理想工作点位于效率最高点处。与螺旋桨敞水效率曲线不同的是，泵高效区较宽，能够适应较大的航速区间变化需求。与螺旋桨一致的是，泵推系统的真实工作点同样位于近高效点的左前方，以考虑流体流动能量损失系数随航速的变化，并留出一定的安全空间。

图2.8　某推进泵转速一定时扬程、功率和效率随流量变化曲线