(一)扩建方案选择模型
1.层次分析法(AHP)确定指标权重
层次分析法的基本思路是将一个复杂的问题分解成若干个组合因素,将这些因素按其系统的支配关系,分组形成递阶层次结构;通过两两比较的方式确定层次结构中诸因素的相对重要性,然后综合人们的经验判断,以决定诸因素相对重要性的顺序和权重。
层次分析法的具体程序分解如下:
(1)建立系统的递阶层次结构。在这一个步骤中,要求将问题所含的要素进行分组,把每一组作为一个层次,并将它们按照“最高层(目标层)—若干中间层(准则层)—最低层(属性层)”的次序排列起来。
(2)建立判断矩阵。这一个步骤是AHP 决策分析中一个关键的步骤。就判断矩阵表示针对上一层次中的某元素而言,评定该层次中各有关元素相对重要性程度的判断,其形式如下:

(3)层次单排序。即在层次分析中由单一判断矩阵计算元素之间相对重要性权重。层次单排序是通过解以下特征值问题得到的:
![]()
式中: λmax 为判断矩阵B 的最大特征根;W 为 λmax 的正规化特征向量,W的分量Wi 就是对应元素单排序的权重值。
运用方根法计算判断矩阵的最大特征值 λmax :
①计算判断矩阵每行所有元素的几何平均值:
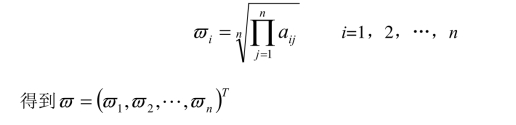
②将 iϖ 归一化,即计算:
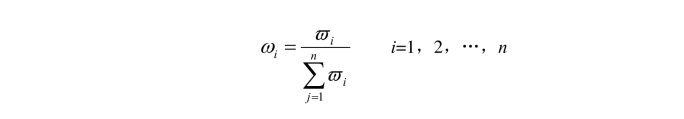
得到ϖ=(ω1,ω2,…ωn)T,即为所求特征向量的近似值,这也是各因素的相对权重。
③计算判断矩阵的最大特征值 λmax :
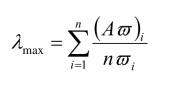
其中,( Aϖ )i为向量 Aω 的第i 个元素。(https://www.xing528.com)
(4)检验判断矩阵的一致性。通过前面的分析,我们知道,如果判断矩阵B具有完全一致性时, λmax =n。但是,在一般情况下是不可能的。为了检验判断矩阵的一致性,需要计算其一致性指标:
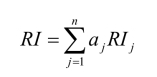
当CI=0 时,判断矩阵具有完全一致性;反之,CI 愈大,就表示判断矩阵的一致性越差。
2.模糊综合评价法
所谓模糊综合评价法,简单地说,就是运用模糊数学和模糊统计方法,通过对影响事物的各个因素的综合考虑,对该事物的优劣做出科学的评价。
(1)模糊综合评判包括六个基本要素。①评判因素论域U。代表综合评判中各评判因素所组成的集合。②评语等级论域V。代表综合评判中评语所组成的集合,它实质是对被评事物变化区间的一个划分,如很好、好、中、差、极差等评语。③模糊关系矩阵R。R 是单因素评价的结果,即单因素评价矩阵。模糊综合评价的对象正是R。④评判因素权向量A。A 代表评价因素在被评对象中的相对重要程度,它在综合评判中用来对R 做加权处理。⑤模糊算子。模糊算子是指合成与所用的计算方法,即合成方法。⑥评判结果向量B。
(2)模糊综合评价的基本方法和步骤。①寻找评价因素集:
U=[u1,u2,…,un]
②对各个影响因素赋权值。各个影响因素对评价对象的影响程度是不一样的。因此在进行评价时,每个元素的重要性程度也不同。为了使评价更具科学性,对各个因素应分别赋予不同值的权值,组成权值集:
A=[a1,a2,…,an]
③确定隶属关系,建立评价矩阵。根据实际情况,寻找因素集中各个元素对备择集中各个元素的隶属关系,建立隶属函数,确定隶属度。单个因素构成一个模糊评判向量,所有单因素的模糊评判向量构成因素模糊评价矩阵:
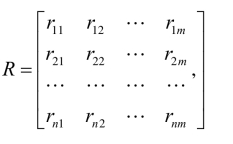
(二)基于模糊层次综合评价法的扩建方案选择
1.AHP 确定指标权重
(1)建立层次结构模型。通过调查扩建方案对项目的影响,认为在进行扩建方案的选择过程中,主要考虑的因素有三个方面:经济合理性、技术可行性、项目服务水平。因此,本书在考虑扩建方案各类影响因素特性的基础上,建立扩建方案选择的层次结构模型,如图3-1 所示,包括目标层A、准则层B、分准则层C 及方案层S。
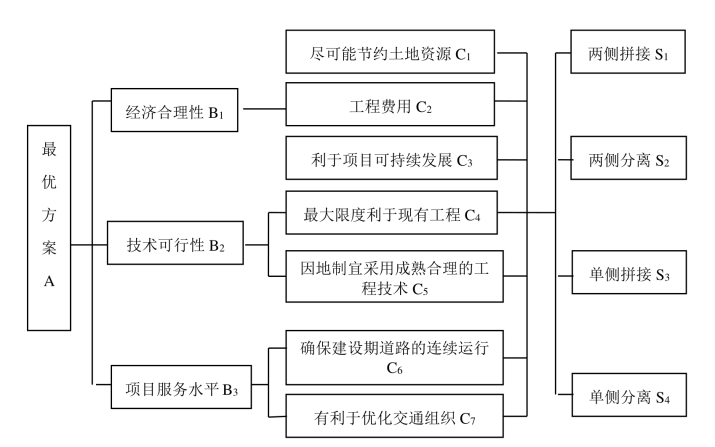
图3-1 扩建方案选择的层次结构模型
(2)构建两两判断矩阵。建立层次分析模型后,上下两层要素制表间的隶属关系就被确定了。对同一层次要素,用上一级的要素为准则进行两两比较。其比较结果以1~9 标度法表示,1 表示同等重要,3 表示稍微重要,5 表示明显重要,7 表示强烈重要,9 表示极端重要,每两者之间的中间级别用2、4、6、8 表示。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




