【摘要】：将称为区间犹豫模糊元，一般情况，区间犹豫模糊元中的元素长度L＞1。X上形如GH={〈x，ghA〉，∈X}的组合，称作灰色犹豫模糊集。其中ghA:X→G[0，1]表示元素x属于集合GH上的所有灰色隶属度构成的集合，称ghA为一个灰色犹豫模糊元。可见，灰色犹豫模糊集是对犹豫模糊集的扩展，可以进一步利用灰色系统理论解决模糊数学难以解决的“小样本”“贫信息”等不确定问题。在应用灰色犹豫模糊多属性决策时，根据各属性的评价值建立决策矩阵。
定义5.2 设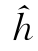
A(x):X→D[0，1]，D[0，1]表示区间[0，1]上的所有闭合的由若干个不同隶属度组成的数据组。集合X上的
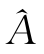={〈x，hA(x)〉
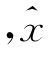∈X}数据组称为区间犹豫模糊集合，可以用IVHFS表示[204]。
将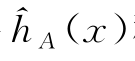
称为区间犹豫模糊元(IVHFE)，一般情况，区间犹豫模糊元中的元素长度L＞1。如果犹豫模糊元中元素长度L=1，则区间犹豫模糊元退化为区间直觉模糊元;如果区间犹豫模糊元中的每一个元素都是实数，则其退化为犹豫模糊元。
定义5.3[205] 令X为某给定的集合，G[0，1]表示在[0，1]上的封闭灰集组合，代表不同的灰色隶属度区间。X上形如GH={〈x，ghA(x)〉，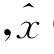
∈X}的组合，称作灰色犹豫模糊集(GHFS)。其中ghA(x):X→G[0，1]表示元素x属于集合GH上的所有灰色隶属度构成的集合，称ghA(x)为一个灰色犹豫模糊元(GHFE)。(www.xing528.com)
如果对于一个灰色犹豫模糊集，任何一个灰色犹豫模糊元都有L=1，则灰色犹豫模糊集退化为灰色模糊集;若其灰色犹豫模糊元中任何一个犹豫模糊数都不是区间数，则灰色犹豫模糊集退化为犹豫模糊集。
可见，灰色犹豫模糊集是对犹豫模糊集的扩展，可以进一步利用灰色系统理论解决模糊数学难以解决的“小样本”“贫信息”等不确定问题。在应用灰色犹豫模糊多属性决策时，根据各属性的评价值建立决策矩阵。设有m个评价对象组成方案集A={A1，A2，…，Am}，n个决策属性组成指标集X={X1，X2，…，Xn}，则灰色犹豫模糊决策矩阵为:
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
