直觉模糊有序加权距离测度及其应用研究

在有些实际情况下，需要在集结数据之前对数据进行排序，对偏差较高和较低的值赋予较小的权重，以减少偏差。例如，跳水和体操比赛中评委打分时，需要对各评委给出的分值进行排序，然后去掉最高分和最低分，把剩下的数据进行加总得到运动员的最终得分。为处理上述问题，基于有序加权算子(OWA)和有序加权距离(OWD)的思想，提出直觉模糊有序加权距离测度(IFOWD)。

定义4.3 设A=(α1，α2，…，αn)和B=(β1，β2，…，βn)为直觉模糊集，则

在IFOWD中，当赋予参数w和λ不同的值时，可以得到IFOWD不同形式的直觉模糊距离测度。

(1)当λ=1时，IFOWD退化为直觉模糊有序加权Hamming距离(IF-OWHD):

在上式中，若对任意的j，权重wj=1/n，则IFOWHD退化为标准直觉模糊Hamming距离(IFNHD)，当dIFD(ασ(j-1)，βσ(j-1))=dIFD(ασj，βσj)(j=1，2，…，n)时，可得直觉模糊加权平均Hamming距离(IFWHD)。

(2)当λ=2时，IFOWD退化为直觉模糊加权Euclidean距离(IFOWED):

此时，若对任意的j，权重wj=1/n，则IFOWHD退化为标准直觉模糊Euclidean距离(IFNED)，当dIFD(ασ(j)，βσ(j))=dIFD(αj，βj)(j=1，2，…，n)时，可得直觉模糊加权平均Euclidean距离(IFWED)。

(3)当λ→0时，可得直觉模糊有序加权几何距离(IFOWGD):

此时，若对任意的j，权重wj=1/n，可得标准直觉模糊几何距离(IFNGD)，当dIFD(α(j)，β(j))=dIFD(αj，βj)(j=1，2，…，n)时，可得直觉模糊加权几何距离(IFWGD)。

受Zhaoetal.[196]、Merigo和Casanovas[197，198]和Gil-Lafuente[199]等学者的启发，可得IFOWD的其他特殊形式，如:

(1)当w1=1，wj=0(j≠1)时，得到两个直觉模糊集的最大距离(MAXD);

(2)当wn=1，wj=0(j≠n)时，得到两个直觉模糊集的最小距离(MIND);

(3)一般地，当wk=1，wj=0(j≠k)时，得到位置直觉模糊距离(Step-IFOWD)。

关于有序加权距离测度IFOWD的一个关键问题是如何确定与之相关联的权重，从定义可见，IFOWD具有有序加权算子的良好性质。可根据IFOWD的特征，给出三种权重确定方法:

(1)设

由上式得到的权重满足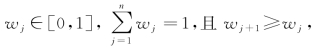因此是风险偏好型心态的权重确定方法，此时决策者持乐观心态。(www.xing528.com)

(2)设

由上式得到的权重满足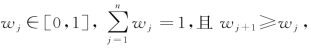因此是风险厌恶型心态的权重确定方法，此时决策者持悲观或谨慎心态。

由上式得到的权重满足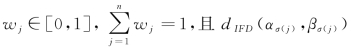越靠近平均值，则其权重越大，此时决策者为风险中性，持中庸心态。

针对实际情况，专家可以根据自己的决策心态或者具体问题特点，应用式(4-10)、(4-11)或(4-13)的赋权法，对IFOWD设定合适的权重，然后进行数据集成，得到较为理想的评价结果。

例4.1 设A=(α1，α2，α3，α4)={(0.8，0.2)，(0.7，0.2)，(0.5，0.4)，(0.3，0.5)}和B=(β1，β2，β3，β4)={(0.5，0.1)，(0.6，0.2)，(0.7，0.1)，(0.4，0.4)}为两个直觉模糊数集，用IFOWD计算两者之间的距离测度。

解:首先计算对应直觉模糊的距离，如-0.1|)=0.2，同理可得:dIFD(α2，β2)=0.05，dIFD (α3，β3)=0.25，dIFD(α4，β4)=0.1。

对以上四个距离从大到小降序排列，有

dIFD(ασ(2)，βσ(2))=dIFD(α1，β1)=0.2

dIFD(ασ(3)，βσ(3))=dIFD(α4，β4)=0.1

dIFD(ασ(4)，βσ(4))=dIFD(α2，β2)=0.05

如果用式(4-11)计算权重，不失一般性，分别考虑λ=1和λ=2的情形，可以计算直觉模糊集A与B之间的有序加权距离:

(1)当λ=1时，有

IFOWD(A，B)=0.42×0.25+0.33×0.2+0.17×0.1+0.08×0.05=0.192;

(2)当λ=2时，有

IFOWD(A，B)=0.42×0.252+0.33×0.22+0.17×0.12+0.08×0.052=0.26。