(1)皮尔逊相关系数
相关关系是不完全确定的随机关系，连续变量间的相关系数用皮尔逊(Pearson)相关系数来测定，两个连续变量X和Y之间的皮尔逊相关系数的计算公式为:
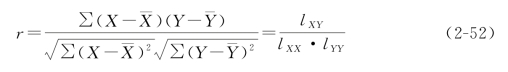
其中，lXX=∑(X-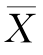
)2，lYY=∑(Y-
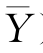)2，lXY=∑(X-
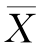)(Y-
)。
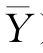r的取值在-1和1之间，r值与变量相关程度之间的关系如表2-3所示。
表2-3 |r|的取值与相关程度
Tab.2-3 |r|-value and degree of correlation
(2)Spearman秩相关系数
假设有容量为n的由两个变量X和Y构成的随机样本，分别计算每个观测关于变量X和Y的秩变量ui和vi (i=1，2，…，n)，用di=ui-vi表示第i个样本对应于两个变量的秩之差，则Spearman秩相关系数的计算公式为:
Spearman秩相关系数的取值也是-1和1之间。计算出Spearman秩相关系数rs后，要对该系数进行检验。检验的原假设为:两变量不相关。在满足原假设的条件下，如果是小样本，则rs服从Spearman分布;在大样本下，统计量z=
近似服从标准正态分布。
(3)Kendall秩相关系数
Kendall秩相关系数是利用变量的秩进行变量之间的一致性趋势检验。假设有容量为n的由x和y两个变量构成的随机样本，首先计算每个观测变量关于变量x和y的秩变量u和v，然后将n个观测变量按变量x升序排列。则n个观测关于变量x和y的秩如下[184]:
x的秩变量u:1，2，…，n;y的秩变量v:v1，v2，…，vn。
设在v1的后面有R1个秩大于v1，v2的后面有R2个秩大于v2，…，在vn-1后面有Rn-1个秩大于vn-1，令:R=R1+R2+…+Rn-1，显然，变量x和y相关性越强，则R越大。
Kendall秩相关系数按如下公式求得:
Kendall秩相关系数的绝对值不超过1。(www.xing528.com)
(4)Wilcoxon符号秩检验
定序变量配对样本间的相关性常用Wilcoxon符号秩检验，Wilcoxon检验利用两个配对组的数值之差进行检验。求出数值差之后，按照绝对值由小到大对这些差值排序。计算最小的秩和，记为T。如果样本配对数目n≤15，则直接将T值与查表得到的临界值比较[185]。
如果n＞15，则T值近似服从正态分布，可以用z分数作为检验统计量。
检验统计量为:
其中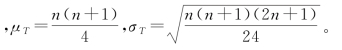
上式中，n为配对数目，T为正值差的秩或负值差的秩中的较小者。
(5)Friedman检验
Friedman 检验是M.Friedman
于1937年提出的，它是随机化区组设计的非参数替代技术。随机化区组设计的假定与方差分析(ANOVA)的假定一样，即观察值是从正态总体中随机抽取的。如果不满足这个假定，或研究对象是排序数据，则应采用Friedman
检验。Friedman 检验有三个基本假定:一是区组相互独立;二是区组与处理之间没有交互效应;三是各区组内的观察值可以进行排序[186]。
待检验的假设如下:
H0:处理总体相同 H1:至少有一个处理总体不同
进行Friedman 检验时，首先把原始数据转换为排名。Friedman检验是在每个区组内分别从1到c进行排序。每个区组都有c个排名，其中c是处理水平数。利用这些排名，Friedman 检验可以判断不同的处理水平(列)是否来自同一个总体。Friedman 检验所用的检验统计量见式(2-56)，该统计量近似服从卡方分布，如果c＞4，或c=3且b＞9，或c=4且b＞4，则自由度为df=c-1。
Friedman 检验的统计量为:
式中，c=处理水平(列数)，b=区组(行)数，j=特定处理水平
-1，Rj=特定处理水平(列)的秩和。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
