TOPSIS法在大学评价中的应用研究成果

TOPSIS法(TechniqueforOrder Preference by SimilaritytoIdealSolution)，直译为逼近理想解法，是Hwang和Yoon于1981年提出的一种适用于根据多项指标对多个研究对象进行比较评价的统计方法。其基本思路是通过构造多指标问题的理想解和负理想解，并以靠近理想解和远离负理想解两个基准作为评价各对象的判断依据，因而也被称为双基准法[182]。

TOPSIS法的具体算法步骤归纳如下:

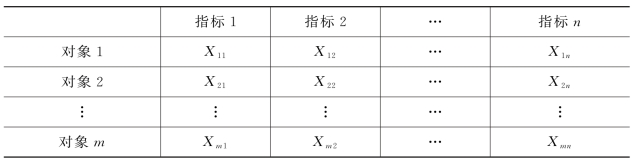
(1)设有m个被评价对象，n个指标，指标值为xij，则决策矩阵为X=(xij)m×n，如表2-2所示。

表2-2 原始数据矩阵
Tab.2-2 Original data matrix

(2)指标的规范化。评价指标中有的是正指标，如效益类指标。有的是逆指标，如成本类指标。评价时要求都具有相同的趋势，一般把逆指标转化为正指标，转化方法可以采用倒数法(即1/x)和差值法(即1-x)。

(3)用向量归一法对决策矩阵作标准化处理，得标准化矩阵Y=(yij)m×n，其中

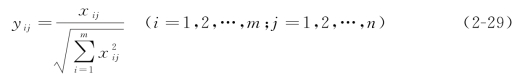
(4)计算加权标准化矩阵。设决策者给出的各属性的权重向量为:

W=(w1，w2，…wn)T，则uij=wj·yij (i=1，2，…，m;j=1，2，…，n)

加权标准化矩阵为:

(www.xing528.com)

(5)确定正理想解和负理想解。

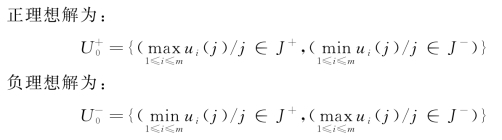
其中，J+表示效益型指标集，J-表示成本型指标集。

(6)计算第i个方案到正理想解、负理想解的距离。

备选方案到正理想解的距离为:

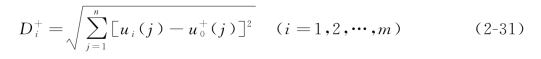
备选方案到负理想解的距离为:

(7)计算各评价对象的相对贴近度:

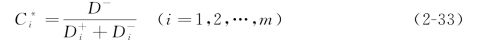
按照相对贴近度大小对被评价对象排序，相对贴近度的值越大，被评价对象越优;反之，相对贴近度的值越小，被评价对象越劣。因此，可以根据的值对各备选方案进行排序和择优。