大学评价中的犹豫模糊集与多属性决策方法

由于群决策时，决策者经常面临不确定性和模棱两可的状态，或是不能相互妥协，使得最终无法取得一致共识。为此，一些学者提出了模糊集的广义形式，其中Torra和Norukawa[3-4]提出了犹豫模糊集(HFS)的概念，对一个集合的元素由不同的隶属度来表示，更好地适应了群决策的需要。

定义2.10 设X为一给定的集合，犹豫模糊集是从X→[0，1]的映射，简记为:A={〈x，h(x)〉，x∈X}。

其中，h(x)是[0，1]中几个犹豫模糊数(HFN)的集合，犹豫模糊数为x∈X属于集合A的隶属度值，显然有HFN∈[0，1]。犹豫模糊元包含了集合中可能的所有犹豫模糊数，各个犹豫模糊元中的数据长度一般情况下不同，可以根据以下方法进行判定比较犹豫模糊元的大小:

设X={x1，x2，…，xn}为一论域，A和B为X上的犹豫模糊集，A={〈xi，hA(xi)〉，xi∈X}，B={〈xi，hB(xi)〉，xi∈X}。集合中的元素通常是次序紊乱的，首先将它们按升序进行排列:令σ:(1，2，…，n)→(1，2，…，n)为一排列，使hσ(i)≤hσ(i+1)，hσ(i)是h中第i大的数。

A和B中元素个数可能不同，令l(hA(xi))，l(hB(xi))分别表示hA(xi)，hB(xi)中元素的个数，li=max{l(hA(xi))，l(hB(xi))}。若l(hA(xi))≠l(hB(xi))，则通过向元素个数较少的集合中重复添加元素，直至两个集合元素个数相等。悲观准则下添加数值最小的元素，乐观准则下添加数值最大的元素。为方便起见，本书计算采用悲观准则。

定义2.11 对任一犹豫模糊元h，称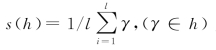为其记分函数，其中l是h中的元素个数。两个犹豫模糊元h1和h2，若s(h1)＞s(h2)，则h1≻h2;若s(h1)=s(h2)，则h1≈h2。

由于几何平均数受极端值的影响比代数平均数小，也可以采用几何平均数作为得分函数。

定义2.12 设h∈H，则称为犹豫模糊集的得分函数，其中l(h)表示集合h中所含元素的个数。若s(h1)＞s(h2)，则h1≻h2;若s(h1)=s(h2)，则h1≈h2。

Torra[3-4]认为犹豫模糊数的两端的隶属包络可以理解为一个直觉模糊数:(www.xing528.com)

定义2.13[3-4] 任一犹豫模糊数h，它的包络(h-，h+)可以用以下公式转换为直觉模糊数:Aenv(h)=(h-，(1-h+))，其中h-=minγ，h+=maxγ，(γ∈h)。

基于犹豫模糊包络关系的内涵，学者[180]研究了两者之间的包络关系集合运算:

在研究了阿基米德T模和S模运算基础上，文献[180]研究了犹豫模糊运算 规则:设存在三个任意犹豫模糊元h，h1和h2，则:

其中l(t)=k(1-t)，且k:[0-1]→[0-∞]为严格递减函数。

犹豫模糊运算规则可以由以下定义给出:

定义2.14[180] 设有任意三个犹豫模糊数h，h1和h2，则:

定义2.15 设A={〈xi，hA(xi)〉，xi∈X}，(i=1，2，…，n)是犹豫模糊集，则A的信息能量定义为: