1.模型假设与简化
采用地下工程通用有限元软件Midas GTS 来建立用于研究盾构开挖施工过程对上部建筑物沉降影响的模型,地下土层采用三维弹塑性实体单元,隧道结构以及建筑桩基均采用三维弹性实体单元,地下土层节点与隧道结构节点共用。假定建筑基础与地下土层接触面之间没有滑动,因此地下土层节点与建筑桩基节点共用。地下土层及岩体本具有复杂性以及不均匀性,想要完全模拟出地下真实情况目前技术还无法达到,因此就要进行合理的假设以及必要的简化,使得模型在考虑时间成本和经济成本的情况下尽可能地模拟出实际情况。
由于岩土材料物理力学特性较为复杂,且隧道周围环境较为复杂,楼房、道路等既有建筑较多,因此实际建模过程中将模型在合理范围内进行假设和简化处理。
(1)假定土体及注浆材料内部均匀,为理想弹塑性体,采用莫尔-库仑屈服准则以三维实体单元进行模拟。
(2)假定土体中不存在构造应力或假定构造应力可忽略不计,因此在模型建立中只考虑土体自重。
(3)隧道管片、等代层采用实体单元进行模拟,盾壳采用2D 板单元进行模拟,按照线弹性计算,不考虑非线性。
(4)由于既有建筑为20 世纪80 年代修建,缺少详细图纸资料,在进行数值模拟时采用等效近似进行计算,上部结构取重度为5 kN/m3 的实体单元进行计算。
(5)由于隧道在下穿既有建筑时弧度较小,因此在模型建立时假设为直隧道。
2.计算参数的选取
本模型采用的材料单元本构模型主要有两种线弹性模型和莫尔-库仑模型,详见表4.2.1。
表4.2.1 材料本构模型

线弹性模型应力与应变之间成线性关系,只需弹性模量和泊松比两个条件。莫尔-库仑模型是经典的土体本构模型,莫尔-库仑模型属于弹塑性模型,在未达到屈服状态条件之前应力与应变成线性关系,当达到屈服阶段之后便会产生不可恢复性变形即塑性变形,需要知道弹性模量、泊松比、黏聚力和摩擦角四个基本条件。从地勘报告以及郑州具体的施工经验可以得到岩土、隧道支护以及建筑结构材料的物理力学参数,如表4.2.2 所示。
表4.2.2 岩土、隧道支护及建筑结构材料物理力学参数表
 (https://www.xing528.com)
(https://www.xing528.com)
3.模型尺寸与网格划分
计算模型边界尺寸沿隧道掘进方向取300 m(长度),宽200 m,深40 m,侧面约束水平位移,底面约束水平和垂直位移,上表面为自由边界。模型中单元共用节点,不设接触。掘进压力取值0.1 MPa,注浆压力取值0.28 MPa。隧道与建筑物相对位置及各部分网格划分情况如图4.2.2~4.2.4 所示。

图4.2.2 隧道与建筑物数值分析模型(一)
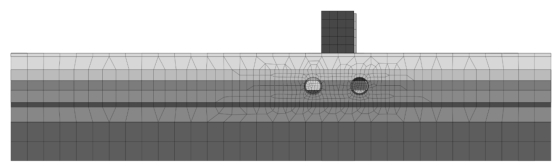
图4.2.3 隧道与建筑物数值分析模型(二)
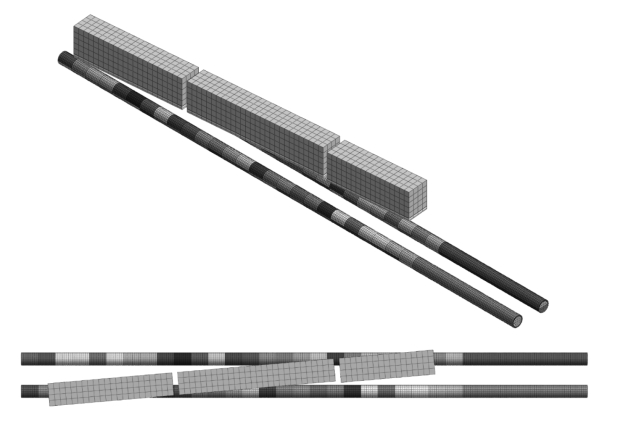
图4.2.4 隧道与房屋侧穿关系
4.定义施工阶段
由于下穿段盾构掘进需要试验段提供相应参数支持,故施工掘进先后顺序为:先行始发花园路站—经三路站左线区间,左线区间掘进100 m 后右线可以进行始发,两台盾构机推荐要求不小于100 m。
该段隧道分为左右两条线路,模型中左右两条隧道长度均为 300m,每节管片长1.5m,本模型主要分析盾构施工引起的地层变形,左线先于右线开挖111 m,其后取9 m 为一个开挖段。施工阶段组划分如下:
初始阶段:激活模型自重和位移边界,位移清零。
隧道开挖:采用钝化的方法模拟土层的开挖,并通过激活已设定好的荷载作用模拟开挖时所需要的掘进压力、千斤顶压力、注浆压力等各种力的作用。由于盾构机长度为 9m,因此当开挖进行到下一段时进行前一段管片的拼装,同时跟进注浆。如此循环进行至最后一节管片拼装结束为止。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




