（1）暂停节点负载重分配。
对于暂停节点，由于过载节点与周边节点所构成的线路依然照常通车，只是交通设施显得“供不应求”，我们考虑在此种情况下，旅客将优先选择节点连边剩余容量较大的线路，这样，将过载节点的多余负载通过边进一步分配给相邻节点，扩大级联效应的影响。基于此，构建考虑边剩余容量的负载重分配模型，见式（6-7）、（6-8）。
式中 Δ ei（jt+1）── t+ 1时刻由暂停节点i 分配至边ij 的负载；
Γi── 节点i 的邻居节点集合。
（2）失效节点负载重分配。
对于失效节点，所有与之相连的线路都将作废，由此将导致此地交通瘫痪。旅客在进行路线选择时，首要考虑的因素便是到达站点的通达程度，其次对于换乘的旅客而言，对应站点在全网中的连通程度也将成为其考虑的重要因素之一。基于此，构建考虑距离和全网连通度的网络连通距离权效应指标，用 fij表示连通距离权效应，见式（6-9）、（6-10）。
式中 Bij── 边ij 的介数；
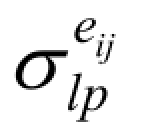── 通过边 eij节点 vl和 vp之间的最短路径数；
σlp── 节点 vl和 vp之间的最短路径数；(www.xing528.com)
Γi── 节点i 失效前的邻居节点集合；
dij── 边ij 的实际空间距离。
据此，构建失效节点的负载重分配模型，见式（6-11）、（6-12）。
式中 Δeij(t+1)── t+ 1时刻由失效节点i 分配至节点j 的负载。
（3）过载连边负载重分配。
对于暂停边，将过量负载平均分配至相邻两节点，假设Δvi为暂停边分配至节点 vi的负载，见式（6-13）。
对于失效边，将负载全部分配至相邻两节点，假设Δvi为失效边分配至节点 vi的负载，见式（6-14）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
