对于框架柱,需要分别计算其在框架平面内和在框架平面外的计算长度。
6.5.2.1 在框架平面内的计算长度
框架柱的稳定应纳入框架的整体失稳一起分析。分析时一般取平面框架作为计算模型,且不考虑空间作用。另外,在分析框架时,还应根据框架有无支撑分为有支撑框架和无支撑纯框架两种类型,而前者还需按支撑结构(桁架、剪力墙、电梯井等)的侧移刚度(产生单位侧倾角的水平力)sb的大小划分为:
强支撑框架
![]()
弱支撑框架
![]()
式中 ∑Nbi、∑N0i——第i层层间所有框架柱用无侧移框架柱和有侧移框架柱计算长度系数μ(见后述)算得的轴心压杆稳定承载力之和。
无支撑纯框架或称为有侧移框架,因其在失稳时产生侧移。弱支撑框架在失稳时亦有一定侧移,而强支撑框架则无侧移。有侧移框架的稳定承载力比相同条件的无侧移框架的低得多。在实际工程中,除了少数设有侧移刚度较大的支撑体系或剪力墙等以外,单层框架一般应按有侧移框架考虑。而多层框架支撑结构的侧移刚度sb通常较易满足式(6.34)的要求,故大多数为强支撑的无侧移框架,即弱支撑框架很少。由此可见,工程中采用的框架多为无侧移框架和有侧移框架这两种失稳形式。
为了简化计算,现在一般对框架结构(不论有无支撑)的稳定仍然采用一阶弹性分析(详见后述),并将框架柱和横梁作为单独构件,仅在计算时考虑其相互约束影响,采用计算长度代换实际长度来反映,即将不同支承情况的构件长度代换为等效铰接支承的长度,用计算长度系数μ来表达。计算时还采用如下假定:①框架只承受作用在节点上的竖向荷载,当荷载作用在横梁上时,也可近似地将荷载移至柱顶,并忽略荷载在梁端引起的弯矩,经这样简化处理所得的计算长度计算柱的强度和稳定时,误差不大;②所有框架柱同时丧失稳定,即各柱同时达到临界荷载;③失稳时,框架两端的转角相等;④只考虑与框架柱相连横梁的约束作用,略去不直接相连横梁的约束作用。且当柱失稳时相交于同一节点的横梁对柱子提供的约束弯矩,按横梁与柱的线刚度之比分配给柱。
(1)单层等截面框架柱在框架平面内的计算长度。
1)有支撑框架。
a.强支撑框架。如图6.18(a)所示的单层单跨等截面柱对称框架,在框架顶部设有防止其侧移的强支撑支承,因此框架在失稳时无侧移,横梁两端的转角θ大小相等,方向相反,呈对称失稳形式。根据弹性稳定理论可计算出无侧移框架的计算长度系数μ,见附表5.2,其值取决于柱底支承情况以及梁对柱的约束程度,后者用K1=I1H/(Il)表达,它代表横梁的线刚度I1/l与柱的线刚度I/H的比值。当横梁与柱铰接时如图6.18(c)所示,取横梁线刚度为零,即K1=0。当横梁的惯性矩很大,即I1→∞,或K1→∞时,它近似于横梁与柱刚接,但考虑到工程实际情况,均按K1≥10的μ值取用。因此,对于与基础刚接的柱,当K1=0~10时,其μ值在0.732~0.549范围。上述数值较图6.18(a)、(c)中的理论值0.5~0.7稍大,原因是当柱与基础刚接时,理论上其K2→∞(详见后述),然而考虑到实际工程中柱脚并非绝对嵌固,故附表5.2中数值实际是取用多层无侧移框架柱的计算长度系数表中K2≥10时的μ值。对于与基础铰接的柱,当K1=0~10时,其μ值在1.0~0.732范围,即附表5.2中数值是取用K2=0时的μ值。

图6.18 单层框架等截面柱的计算长度系数μ
对单层多跨强支撑框架如图6.19(a)所示,在失稳时同样可假定横梁两端转角θ大小相等方向相反,且各柱失稳在同时产生,其计算长度系数μ亦可采用附表5.2。但表中K1=(I1/l1+I2/l2)/(I/H),即采用与柱相邻的两根横梁线刚度之和与柱线刚度的比值。
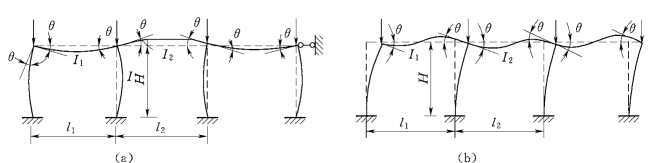
图6.19 单层多跨框架失稳形式
(a)无侧移;(b)有侧移
b.弱支撑框架。弱支撑框架的框架柱可直接按下式计算出的轴心压杆稳定系数进行计算
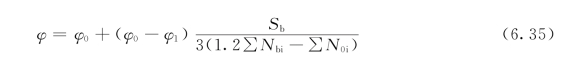
式中 φ1、φ0——用无侧移框架柱和有侧移框架柱计算长度系数算得的轴心压杆稳定系数。
2)无支撑纯框架。无支撑纯框架应按有侧移框架考虑。分析有侧移框架的内力目前有两种方法:一种为框架的内力采用一阶弹性分析方法,即不考虑框架结构变形对内力产生的影响,根据未变形结构建立平衡条件,计算框架由各种荷载产生的内力,然后将框架柱作为单独的压弯构件进行设计,而框架在平面内的稳定计算则用框架柱的计算长度l0=μl来考虑与柱相连构件的约束影响,因此一阶分析只是一种简化的近似方法;另一种是二阶弹性分析方法,它是根据变形后的框架结构建立平衡条件。即考虑结构变形对内力产生影响的P-Δ效应(二阶效应),故而框架在平面内的稳定计算采用框架柱的实际几何长度L,即μ=1.0。
从以上所述可见,二阶分析是一种精确的计算方法,但其分析较繁,且计算工作量较大(需借助电算)。一阶分析并采用计算长度计算虽是一种近似方法,但其误差值与框架柱的轴心压力N、水平力H和侧移Δu的大小有关。对轴心压力和水平力不太大且侧向刚度较大的单层框架,其误差不大。当与上述情况相反时,其误差才较大。因此,《钢结构设计规范》规定对所有框架结构内力均可采用一阶分折,只对符合下式条件的框架,则推荐宜采用二阶分析,以提高精确度。

式中 ∑N——所计算楼层各柱轴心压力设计值之和(对单层框架为各框架柱轴心压力设计值之和);
∑H——产生层间侧移Δu的所计算楼层及以上各层的水平力之和(对单层框架为产生柱顶水平位移Δu的水平力之和);
Δu——按一阶弹性分析求得的所计算楼层的层间侧移(对单层框架为柱顶水平位移)。
下面对无支撑纯框架的一阶分析、二阶分析两种方法分别加以论述。
a.一阶弹性分析方法。单层框架有侧移失稳的变形是反对称的,横梁两端的转角θ大小相等方向相同。对单层单跨框架柱如图6.20(d),按弹性稳定理论分析的计算长度系数见附表5.1,如对与基础刚接的柱,取K2≥10数值,即当K1=0~10时,其μ值在2.0~1.0范围如图6.20(b)、(c)所示。对与基础铰接的柱,取K2=0数值,其μ值都大于2.0,且变动范围很大。对单层多跨有侧移框架柱如图6.18(b)所示,其计算长度系数同样可用K1=(I1/l1+I2/l2)/(I/H)查附表5.1。

图6.20 单层单跨框架有侧移失稳
b.如前所述,符合判别式(6.36)条件的框架,宜采用二阶分析法分析内力,所以在计算前首先应采用其进行判别。式中的Δu可用框架柱顶水平位移的容许值[Δu]代换(无桥式吊车和有桥式吊车单层框架的[Δu]分别为H/150和H/400,H为自基础顶面到柱顶的总高度)。若公式左侧算出的值大于1.0,则宜采用二阶分析。否则,仍可采用一阶分析。
另外,在采用二阶分析时,还需引入一个考虑各种缺陷(初弯曲、残余应力、安装误差等)的假想水平力(或称概念荷载),用其和实际的水平力及垂直荷载一起对框架进行内力分析。假想水平力作用于每层柱的柱顶(对单层框架为框架柱顶),其计算公式为

式中 Qi——第i楼层的总重力荷载设计值;
ns——框架总层数,当![]() 时,取此根号值为1.0;(https://www.xing528.com)
时,取此根号值为1.0;(https://www.xing528.com)
αy——钢材强度影响系数,Q235钢为1.0,Q345钢为1.0,Q390钢为1.2,Q420钢为1.25。
(2)多层多跨等截面框架柱在框架平面内的计算长度。对多层多跨等截面框架亦需按有支撑框架和无支撑纯框架分类。对有支撑框架还需按判别式(6.33)或式(6.34)判定其为强支撑框架或弱支撑框架。对强支撑框架可按无侧移失稳形式[见图6.21(a)]采用一阶分析确定计算长度系数,对弱支撑框架则按式(6.35)直接计算框架柱的轴心压秆稳定系数。对无支撑纯框架均应按有侧移失稳形式[图6.21(b)]分析,但也需要先用判别式(6.36)判定框架是否宜用二阶分析。若判定需采用二阶分析,则用式(6.37)计算出每层柱顶附加的假想水平力Hni,然后和实际的水平力Hi以及垂直荷载qi等共同作用。
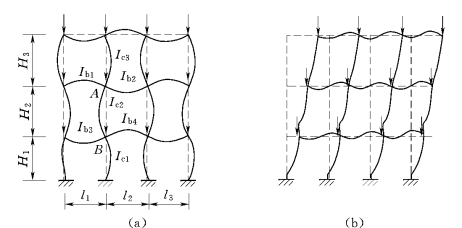
图6.21 多层多跨框架失稳形式
(a)无侧移;(b)有侧移
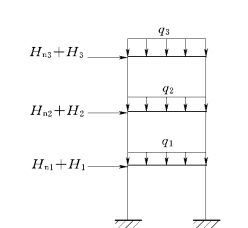
图6.22 无支撑纯框架计算简图
对框架内力进行计算(图6.22),此时取框架柱的μ=1.0。二阶弹性分析可采用近似计算方法,即各杆件的杆端弯矩可近似地用一阶分析的无侧移时杆端弯矩加上有侧移时杆端弯矩乘以弯矩增大系数,详见《钢结构设计规范》。若判定为可采用一阶分析,则按一阶弹性分析方法计算其计算长度系数。
对多层多跨等截面框架采用一阶分析时采用的基本假定同单层多跨框架,但同时还假定在柱失稳时,相交于每一节点的横梁对柱的约束程度,按上、下两柱线刚度之比分配给柱。其计算长度系数亦采用查附录5,表中K1为相交于柱上端的横梁线刚度之和与柱线刚度之和的比值;K2则为相交于柱下端的横梁线刚度之和与柱线刚度之和的比值。当K2=0,即附表5.1中柱与基础铰接的μ值;K2=10即柱与基础刚接的μ值。
如图6.21(a)中柱AB

![]()
6.5.2.2 在框架平面外的计算长度
当框架柱在框架平面外失稳时,可假定侧向支承点(柱顶、柱底、柱间支撑、吊车梁等)是其变形曲线的反弯点。在一般情况,框架柱在柱脚及支承点处的侧向约束均较弱,故均应假定为铰接。因此,在框架平面外的计算长度等于侧向支承点之间的距离见图6.23(a)。若无侧向支承时,则为柱的全长见图6.23(b)。
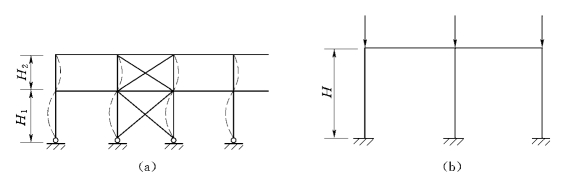
图6.23 框架柱在框架平面外的计算长度
【例6.2】 试确定图6.24所示双跨等截面框架柱(边柱和中柱)在框架平面内的计算长度,柱与基础铰接,按有侧移失稳形式计算。
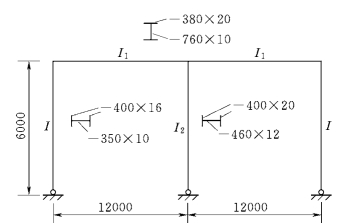
图6.24 例6.2图
解:各构件的惯性矩:
横梁
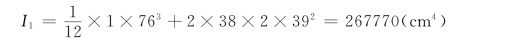
边柱
![]()
中柱
![]()
边柱线刚比
![]()
查附表5.1得 μ=2.12
边柱计算长度
H0=2.12×6=12.72(m)
中柱线刚比应计入两根横梁的线刚度
![]()
查附表5.1得 μ=2.13
边柱计算长度
H0=2.13×6=12.78(m)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




