简支梁沿跨度改变截面后挠度计算成果

图5.48是沿跨度改变截面后简支梁的计算简图，图上x为理论改变点的位置，截面改变前后的惯性矩各为I和I1，梁跨度为l。此时最大挠度将较按惯性矩取I的等截面梁计算时有所增加。挠度公式为

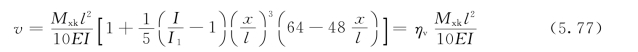
式中　mxk——跨中最大弯矩的标准值；

ηv——挠度增大系数，即式中的方括弧部分。

【例5.6】　试改变例5.5中焊接工字形板梁两端的翼缘板宽度。

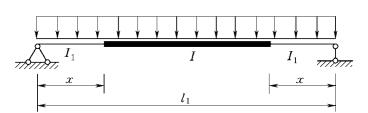
图5.48　改变截面的简支梁

解:（1）试在离支座L/6处改变翼缘板的宽度。在x＝L/6＝9/6＝1.5（m）处梁截面弯矩设计值为

需要翼缘面积

改变后的翼缘板宽度为

说明在离支座L/6处改变翼缘板的宽度，是改变后的板宽过小，不实用。

（2）今取改变后的翼缘板宽度

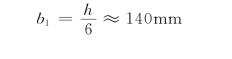
取改变后的截面为

1－8×800　（腹板）

2－14×140　（翼缘板）

示于图5.49。

惯性矩　

截面模量　

改变后截面能抵抗的弯矩

M1＝γxfWx1＝1.05×215×2393×103×10－6＝540.2（k N·m）(www.xing528.com)

使　

即　

亦即　0.66x2－284.3x＋540.2＝0

理论改变点为

（3）实际改变点为

（4）截面改变后的挠度验算。挠度增大系数为

图5.49　翼缘截面的改变

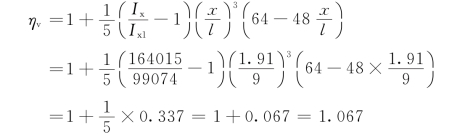
由例5.5的，得改变翼缘宽度后梁的相对挠度增量为

（5）在理论改变点，弯曲应力突然加大，因此需验算该截面腹板边缘处的折算应力。

折算应力　

＜1.1f＝1.1×215＝236.5（N/mm2）

（6）翼缘截面改变后节省的钢材估算。等截面焊接工字形板梁的钢材体积为

AL＝142.4×10－4×9＝0.12816（m3）

翼缘截面改变后节省的钢材体积为（见图5.49）

节省钢材的百分比为