【摘要】:图5.46所示为一在均布荷载作用下的简支梁。在理论改变点距支座为x处,上、下翼缘板宽度由b改变为b1,每一翼缘板的截面积由Af改变为Af1。梁左右两端,上、下翼缘板改变截面后理论上共节约钢材体积为式中,x=al。图5.46组合钢梁翼缘板宽度的改变应确定改变后的翼缘面积Af1或翼缘板宽度b1。通常可先求出理论改变处截面上的最大弯矩,然后由式求出Af1的近似值。因式是近似的,所以确定Af1或b1后,还要对其进行抗弯强度和折算应力的验算。
(1)应确定改变翼缘宽度的位置,确定的根据是使节省的翼缘钢材为最多。图5.46所示为一在均布荷载作用下的简支梁。在理论改变点距支座为x处,上、下翼缘板宽度由b改变为b1,每一翼缘板的截面积由Af改变为Af1。梁左右两端,上、下翼缘板改变截面后理论上共节约钢材体积为
![]()
式中,x=al。
跨度中点的最大弯矩和截面模量为
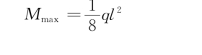
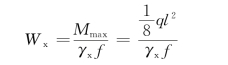
理论改变截面处的弯矩和截面模量为
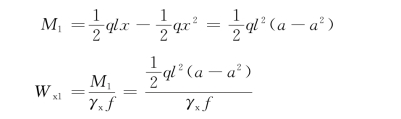
利用近似式(5.74),可得
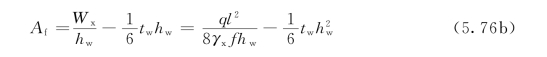
和![]() (https://www.xing528.com)
(https://www.xing528.com)
故![]()
代入式(5.76a),得节省的钢板体积为
![]()
由![]() ,得 1-8α+12α2=0
,得 1-8α+12α2=0
解得![]() 或
或![]() ,后者无意义,故得简支梁翼缘截面改变的理论地点应在距支座
,后者无意义,故得简支梁翼缘截面改变的理论地点应在距支座![]() 处。此值虽导自均布荷载作用下,设计中对其他荷载(如吊车荷载等)作用下也可采用
处。此值虽导自均布荷载作用下,设计中对其他荷载(如吊车荷载等)作用下也可采用![]() 。
。
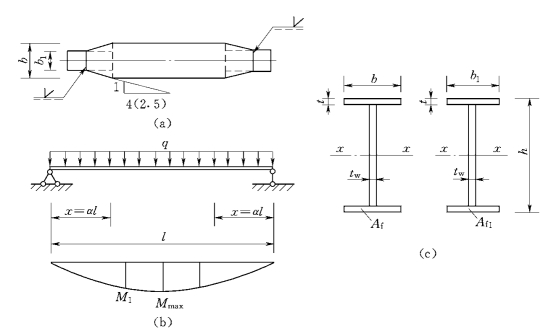
图5.46 组合钢梁翼缘板宽度的改变
(2)应确定改变后的翼缘面积Af1或翼缘板宽度b1。通常可先求出理论改变处截面上的最大弯矩,然后由式(5.74)求出Af1的近似值。因式(5.74)是近似的,所以确定Af1或b1后,还要对其进行抗弯强度和折算应力的验算。
为了避免在理论改变点因突然改变截面而产生严重的应力集中,《规范》第8.2.4条中规定:应在宽度方向从两侧做成不大于1∶2.5的斜坡逐渐由b过渡到b1,见图5.46(a)(对直接承受动力荷载还需验算疲劳的梁,斜角坡度不应大于1∶4)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




