工字形板梁腹板区格在弯曲应力作用下的临界应力解析

图5.16一四边简支板在纯弯曲下的屈曲情况。在板的横向屈曲成一个半波；在板的纵向根据板的长宽比a/h0不同，可能屈曲成一个半波或多个半波。其临界应力为

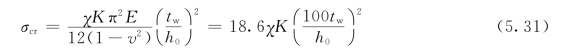
式中，屈曲系数K取最低值23.9，适用于四边简支a/h0＞0.7不论屈曲成一个或若干个半波时，如图5.16所示。对工字板梁的腹板，其下边缘与受拉翼缘相连，因而接近于固定边；其上边缘与受压翼缘的连接，不能笼统的视为固定边。一般按两个情况来确定:当梁的受压翼缘连有刚性铺板、制动板或焊有钢轨时，受压翼缘的扭转变形受到约束，其上边缘可视为完全固定，取χ＝1.66；当受压翼缘扭转未受到约束或约束较弱时，只能视上边缘为简支，取χ＝1.23。

式（5.31）是理想情况下弹性工作阶段的临界应力，腹板实际屈曲时可能已处于非弹性阶段，同时腹板中可能存在各种初始缺陷。因此应与研究轴心受压构件整体稳定性一样，必须引进新的参数即通用高厚比以考虑非弹性工作和初始缺陷的影响。

腹板通用高厚比是:钢材受弯、受剪或受压的屈服强度除以相应的腹板区格抗弯、抗剪或局部承压弹性屈曲临界应力之商的平方根。以受弯区格为例，其通用高厚比为

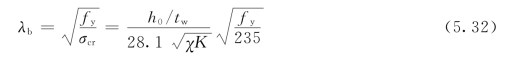
当梁受压翼缘扭转受到约束时，取χ＝1.66，K＝23.9，得

当梁受压翼缘扭转未受到约束时，取χ＝1.23，K＝23.9，得

由通用高厚比的定义可得弹性阶段临界应力σcr与λb的关系必然是

(www.xing528.com)

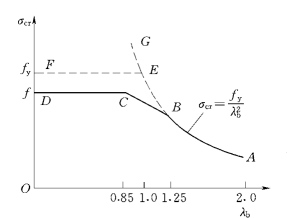
图5.17　纯弯曲时矩形腹板区格的临界应力曲线

其曲线见图5.17中的ABEG线，此线与σcr＝fy的水平线相交于E点，相应的λb＝1.0。ABEF线是理想情况下的σcr—λb曲线。考虑初始缺陷后，我国钢结构设计规范[4]中对纯弯曲下腹板区格的临界应力曲线采用如图5.17中的ABCD线所示。该曲线由三段组成:AB线为一双曲线，表示弹性工作时的临界应力；CD段为一水平直线，表示σcr＝f；BC线为一直线，是由弹性阶段过渡到临界应力等于钢材的强度设计值f（f＝fy/γR）的临界应力曲线。上、下分界点C点和B点的λb分别取为0.85和1.25。

《规范》规定:在弯曲应力作用下的临界应力σcr按下列公式计算:

当λb≤0.85时

当0.85＜λb≤1.25时

当λb＞1.25时

式中　

式（5.35a）和式（5.35b）分别为受压翼缘扭转受到约束和不受约束时的腹板通用高厚比。hc是梁弯曲时腹板的受压区高度。当梁截面为双轴对称时，h0＝2hc，当为加强上翼缘的单轴对称截面时，h0＞2hc，以2hc代替式（5.33）中的h0，可提高腹板屈曲临界应力。由于腹板区格局部失稳的主要因素是弯曲受压区，用2hc代替h0是合理的。同时应注意式（5.34）中，式（a）已考虑了抗力分项系数γR，因而式（a）中原来的σcr＝fy改为σcr＝f，而式（c）中原为σcr＝fy/λ2b改为σcr＝1.1f/λ2b，相当于未考虑抗力分项系数，这是由于当板处于弹性状态时存在较大的屈曲后强度，安全系数可小一些，只保留荷载分项系数就够了。下面将介绍的τcr和σc，cr亦均如此，以后不再说明。图5.17中用B—C—D线代替理论上的B—E—F线，既考虑了非弹性工作，也适当考虑了缺陷的影响。