钢结构中主要影响稳定性的因素

通过式（5.25）所示钢梁整体稳定性临界弯矩公式，可以看到影响临界弯矩大小的因素有:

（1）梁侧向无支长度或受压翼缘侧向支承点的间距l1有关，l1愈小，则整体稳定性能愈好，临界弯矩值愈高。

（2）梁截面的尺寸，包括各种惯性矩，惯性矩Iy、It和Iw愈大，则梁的整体稳定性能就好，特别是梁的受压翼缘宽度b1的加大，还可使式（5.25）中的βy加大，因而可大大提高梁的整体稳定性能。

（3）梁端支座对截面的约束，支座如能提供对截面y轴的转动约束，梁的整体稳定性能可大大提高。由表5.2，当对y轴为固定端时，μ＝0.5，亦即可使梁的临界弯矩提高近3倍。支座如能提供对x轴的转动约束，对临界弯矩的提高也有作用。

（4）梁所受荷载类型。假设梁的两端为简支，荷载均作用在截面的剪切中心处[此时式（5.25）中的α＝0]，梁截面形状为双轴对称工字形且尺寸一定，由式（5.25）可见此时临界弯矩Mcr的大小就只取决于系数C1。由表5.2所示典型荷载的C1值，其中以纯弯曲（弯矩图形为矩形）的C1为最小，跨度中点一个集中荷载（弯矩图形为一等腰三角形）的C1为最大，满跨均布荷载（弯矩图形为一抛物线）的C1居中。

这里之所以特别说明弯矩图形状与系数C1的关系，主要是为了说明梁的临界弯矩大小与荷载类型有关。设计规范中只能列举几种典型的荷载，而实际工程中可能碰到的荷载情况则各种各样。设计时除非是自己计算临界弯矩，如需选用规范中的公式，就应选用与规范中规定最相接近的情况，否则将产生过大的误差。现用图5.11所示的3个例子以作说明:图5.11（a）所示是简支梁承受多个集中荷载而且其位置较为分散，多边形的弯矩图较接近于抛物线，故以按规范中的“均布荷载”考虑为宜；图5.11（b）所示虽是2个或3个集中荷载，但其位置较集中于跨中，弯矩图形较接近于等腰三角形，故以选用规范中的“集中荷载”为宜；图5.11（c）虽然也是两个集中荷载，但其位置靠近梁的两端，弯矩图形较接近于矩形，故以按规范中的“纯弯曲”为宜（图5.11所示两集中荷载作用于l/4跨时，C1＝1.04，已接近于C1＝1.0）。这些都需由设计者自行判断确定。

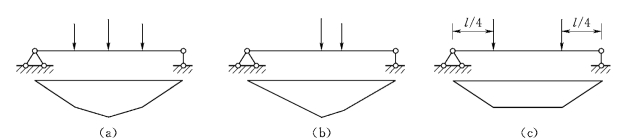
图5.11　非典型荷载时的处理(www.xing528.com)

（a）M图接近抛物线；（b）M图接近三角形；（c）M图接近矩形

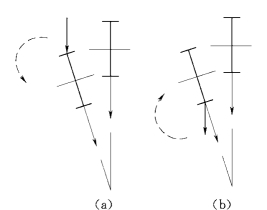
图5.12　荷载作用点高度不同对梁稳定的影响

（a）荷载使梁截面加剧转动；（b）荷载能减少梁截面的转动

（5）沿梁截面高度方向的荷载作用点位置。作用点位置不同，临界弯矩也因之而异。荷载作用于梁的上翼缘时，式（5.25）中α值为负，临界弯矩将降低；荷载作用于下翼缘时，α值为正，临界弯矩将提高。由图5.12也可以看出，当荷载作用在梁的上翼缘时，荷载对梁截面的转动有加大作用因而降低梁的稳定性能；反之，则提高梁的稳定性能。

了解了影响梁整体稳定性的因素后，除可做到正确使用设计规范外，更重要的是可在工程实践中设法采取措施以提高梁的整体稳定性能。