钢结构横向荷载下工字形截面梁的临界弯矩

单轴对称工字形截面[图5.10（a）和图5.10（c）]的剪切中心S与形心O不相重合，承受横向荷载时梁的中性平衡状态微分方程不是常系数，因而不可能有准确的解析解，只能有数值解和近似解。为了便于讨论，下面给出用能量法求得的临界弯矩近似解

图5.10　焊接工字形截面

（a）加强受压翼缘的工字形截面（βy＞0，y0＜0）；（b）双轴对称工字形截面（βy＝0，y0＝0）；（c）加强受拉翼缘的工字形截面（βy＜0，y0＞0）

式中，C1、C2和C3是随荷载类型及支座情况而异的系数，表5.2给出了对截面强轴x可以自由转动的两端简支梁在3种典型荷载情况下的各个C1～C3值:l0＝μl1是梁的侧向计算长度；l1是梁的侧向无支长度；μ为侧向计算长度系数。见表5.2。

表5.2　两端简支梁侧扭屈曲临界弯矩式（5.25）中的系数

(www.xing528.com)

α是荷载在截面上的作用点与截面剪切中心S间的距离，当荷载作用点位于剪切中心上方时，α为负值，反之为正值

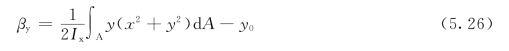
式（5.26）是反映截面单轴对称特性的函数；当截面为双轴对称时，βy＝0；当为加强受压翼缘工字形截面时，βy为正值；当为加强受拉翼缘工字形截面时，βy为负值，见图5.10。式（5.26）中的y0是剪切中心S的坐标为

式中　I1、I2——受压翼缘和受拉翼缘对y轴的惯性矩，Iy＝I1＋I2。

当双轴对称截面时，y0＝0；当为单轴对称工字形截面时，y0＜0或y0＞0，见图5.10。