钢结构：格构式轴心受压构件的整体稳定

格构式受压构件也称为格构式柱，其分肢通常采用槽钢和工字钢，构件截面具有对称轴见图4.1。当构件轴心受压丧失整体稳定时，不大可能发生扭转屈曲和弯扭屈曲，往往发生绕截面主轴的弯曲屈曲。因此计算格构式轴心受压构件的整体稳定时，只需计算绕截面实轴和虚轴抵抗弯曲屈曲的能力。

4.6.2.1　格构式构件绕实轴的整体稳定

格构式轴心受压柱对实轴的稳定计算与实腹柱完全相同，因为它相当于两个并列的实腹柱。但格构柱虚轴的稳定性却比具有同样长细比的实腹柱稳定性小。因为格构柱的分肢是每隔一定距离用缀件连接起来的，缀条或缀板的变形，助长了柱的屈曲变形，所以与实腹柱相比，虚轴方向临界力较低。

为考虑缀件变形对临界力降低的影响，根据理论推导，设计计算时采用加大的换算长细比来代替整个构件对虚轴的实际长细比，这样也就相当于降低了虚轴方向的临界力。采用换算长细比的办法使格构柱的计算大为简化，因为格构柱对实轴稳定计算已与实腹柱相同，而对虚轴的稳定计算，只需用换算长细比查取φ值，其余并无差别。

缀材有缀条和缀板两种。缀条用斜杆组成，也可用斜杆和横杆共同组成，一般用单角钢作缀条，而缀板通常用钢板做成。

轴心受压格构式构件的设计与轴心受压实腹构件相似，应考虑强度、刚度（长细比）、整体稳定和局部稳定（分肢肢件的稳定和板件的稳定）几个方面的要求，但每个方面的计算都有其特点；此外，轴心受压格构式构件的设计还包括缀材的设计。

4.6.2.2　格构柱绕虚轴的换算长细比

格构柱绕实轴的稳定计算与实腹式构件相同，但绕虚轴的整体稳定临界力要低于长细比相同的实腹式构件。

轴心受压构件整体弯曲后，沿杆长各截面上将存在弯矩和剪力。对实腹式构件，剪力引起的附加变形很小，对临界力的影响只占3/1000左右。因此，在确定实腹式轴心受压构件整体稳定的临界力时，仅仅考虑了由弯矩作用所产生的变形，而忽略了剪力所产生的变形。对于格构式柱，当绕虚轴失稳时，情况有所不同，因肢件并不是连续的板而只是每隔一定距离用缀条或缀件联系起来。柱的剪切变形较大，剪力造成的附加挠曲影响就不能忽略。在格构式柱的设计中，对虚轴失稳的计算，常用加大长细比的办法来考虑剪切变形的影响，加大后的长细比称为换算长细比。

《钢结构设计规范》中对缀条柱和缀板柱采用不同的换算长细比计算公式。

（1）双肢缀条柱的换算长细比。

根据弹性稳定理论，当考虑剪力的影响后，其临界力可为:

式中　γ——单位剪力作用下的轴线转角；

λox——格构柱绕虚轴临界力换算为实腹柱临界力的换算长细比

图4.22（a）表示两分肢用缀条联系的格构式轴心受压构件的受力和变形情况。现取出一个缀条节间进行分析，以求出单位剪切角γ。如图4.22（b）所示，在单位剪力V1＝1作用下。设一个节间内两侧斜缀条的面积之和为A1，其内力Nd＝1/sinα；斜缀条长ld＝l1/cosα，则斜缀条的轴向变形为:

假设变形和剪切角是有限的微小值，则由Δd引起的水平变位Δ为:

故剪切角:　

式中　α——斜缀条与柱轴线间的夹角，代入式（4.28）中得:

图4.22　缀条柱的剪切变形

图4.23　缀板柱的剪切变形

在α＝40°～70°的范围内，π2/sin2αcosα＝25.6～32.7。为简化计算，《钢结构设计规范》统一规定使用27，由此得简化式为:

式中　λx——整个柱对虚轴的长细比；

A——整个柱的毛截面面积。

《钢结构设计规范》规定α应在40°～70°之间。当α不在此范围之内时，式（4.33）的误差较大，宜采用式（4.32）计算。还应当注意的是:推导公式（4.33）时，仅考虑了斜缀条由于剪力作用的轴向伸长产生的节间相对侧移，而没有考虑横缀条轴向缩短对相对侧移的影响。因此，式（4.32）和式（4.33）仅适用于不设横缀条或设横缀条但横缀条不参加传递剪力的缀条布置；当用于横缀条参加传递剪力的缀条布置时，式（4.32）和式（4.33）中，还应当补入横缀条（截面面积总和A2）变形影响项，其值为。

由图4.23表示缀板式轴心受压格构式构件的弯曲屈曲变形（包括弯曲和剪切变形）情况，内力和变形可按单跨多层刚架进行分析，并假设反弯点在各层分肢和每个缀板（横梁）的中点，如图4.23（a）所示。若只考虑分肢和缀板在横向剪力作用下的弯曲变形，其分离体如图4.23（b）所示，可得单位剪力作用下缀板弯曲变形引起的分肢变位Δ1为:(www.xing528.com)

分肢本身弯曲变形时的变位Δ2为:

由此得剪切角γ:

将此γ值代入式（4.28），并令K1＝I1/l1，Kb＝Ib/a，得换算长细比λox为:

假设分肢截面面积A1＝0.5A，A1/I1＝，则:

式中　λ1——分肢的长细比，i1为分肢弱轴的回转半径，l01为缀板间的净距离λ1＝l01/i1；

K1——一个分肢的线刚度。l1为缀板中心距，I1为分肢绕弱轴的惯性矩K1＝I1/l1；

Kb——两侧缀板线刚度之和。即Ib为两侧缀板的惯性矩，a为分肢轴线间的距离Kb＝Ib/a。

根据《钢结构设计规范》的规定，缀板线刚度之和Kb应大于6倍的分肢线刚度，即Kb/K1≥6。若取Kb/K1＝6，则式（4.34）中的。因此规范规定柱的换算长细比采用:

当缀件为缀板时:

当缀件为缀条时:

式中　λx——整个构件对x轴的长细比；注意:虚、实轴与X（Y）轴的对应；

λ1——分肢对最小刚度轴1—1的长细比，其计算长度取为:焊接时，为相邻两缀板的净距离；螺栓连接时，为相邻两缀板边缘螺栓的距离；

A1——构件截面中垂直于x轴的各斜缀条毛截面面积之和。

（2）四肢组合构件

当缀件为缀板时:

当缀件为缀条时:

式中　λy——整个构件对y轴的长细比；

A1y——构件截面中垂直于y轴的各斜缀条毛截面面积之和。

（3）缀件为缀条的三肢组合构件

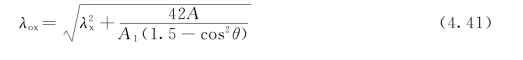
式中　A1——构件截面中各斜缀条毛截面面积之和；

θ——构件截面内缀条所在平面与x轴的夹角。