钢结构:轴心受压构件的屈曲和弯曲

对于轴心受压构件，只有极短的压杆，或者局部有较大孔洞削弱的压杆，才会因截面的平均应力达到设计强度而丧失承载能力，致使强度计算起控制作用。一般来说，轴心受压杆件的承载力是由稳定条件决定的。

稳定和强度是两个不同的概念。轴心受压构件的屈曲（即构件丧失整体稳定）具有突然性，以往国内外因压杆突然丧失稳定而导致重大工程事故的例子是屡见不鲜的，因而，必须引起足够的重视。

杆在轴心压力作用下发生屈曲，屈曲变形可能有三种形式:

（1）弯曲屈曲。杆轴线由直线变为曲线，这时杆的任一截面均绕一个主轴弯曲如图4.6（a）所示。

（2）扭转屈曲。不受约束的截面均绕杆轴扭转如图4.6（b）所示。

（3）弯扭屈曲。在产生弯曲屈曲变形的同时伴有扭转屈曲变形如图4.6（c）所示。轴心压杆可能产生什么样的屈曲形式，主要取决于杆截面的形式和尺寸、杆的长度和杆端的连接条件。

钢结构中常用截面的轴心受压构件，由于其板件较厚，构件的抗扭刚度也相对较大，失稳时主要发生弯曲屈曲；单轴对称截面的构件绕对称轴弯扭屈曲时，当采用考虑扭转效应的换算长细比后，也可按弯曲屈曲计算。因此弯曲屈曲是确定轴心受压构件稳定承载力的主要依据，本节将主要讨论弯曲屈曲问题。

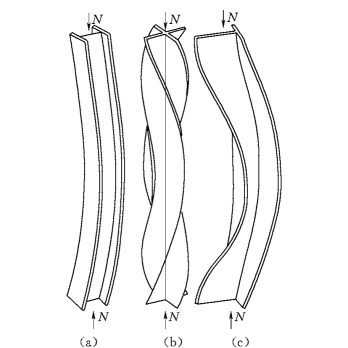
图4.6　两端铰接轴心受压构件的屈曲状态

（a）弯曲屈曲；（b）扭转屈曲；（c）弯扭屈曲

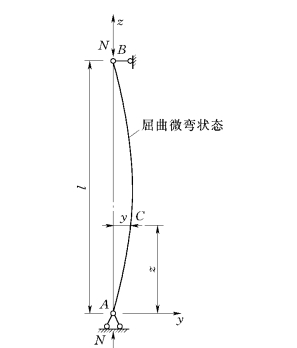
图4.7　轴心受压构件的弯曲屈曲

4.3.1.1　理想轴心受压构件的屈曲

（1）弹性屈曲。图4.7为两端铰接的理想等截面构件，在压力N小于临界力时保持压而不弯的直线平衡状态，当轴心压力N达到临界值时，处于屈曲的微弯状态。在弹性微弯状态下，由内外力矩平衡条件，可建立平衡微分方程，求解后可得到著名的欧拉临界力和相应得临界应力公式为:欧拉临界力为

欧拉临界应力为

式中　E——材料的弹性模量；

I——截面绕主轴的惯性矩；

l、l0——构件的几何长度和计算长度；

μ——构件的计算长度系数，根据构件的端部条件确定，对常见的端部条件，按表4.3采用，考虑到理想条件难于完全实现，表中给出了用于实际设计的建议值；

λ——构件的有效长细比，λ＝l0/i，为截面的回转半径；

A——构件的毛截面面积。

表4.3　轴心受压构件的计算长度系数μ

由式（4.5）可见，压杆的临界力Ncr与构件的弯曲刚度EI成正比，与构件的计算长度l0的平方成反比，而与材料的强度无关。因此，采用高强度材料，并不能提高Ncr值，而只有用增大截面的惯性矩I或减少计算长度l0等措施来提高构件的稳定性。式（4.6）表明临界应力σE与长细比λ的平方成反比，即λ越大，σE就越小，压杆的稳定性就越差。

在欧拉临界力公式的推导中，假定材料无限弹性、符合虎克定律（弹性模量E为常量），因此当截面应力超过钢材的比例极限fP后，欧拉临界力公式不再适用，式（4.6）需满足

或

式中　λp——相应于截面应力为比例极限fP时构件的长细比。

只有长细比较大（λ≥λp）的轴心受压构件，才能满足式（4.7）的要求。对于长细比较小（λ≤λp）的轴心受压构件，截面应力在屈曲前已超过钢材的比例极限，构件处于弹塑性阶段，应按弹塑性屈曲计算其临界力。

（2）弹塑性屈曲。当σcr＞fp，即λ＜λp时压杆的工作已进入非弹性范围，此时，材料的σ—ε关系成为非线性[见图4.8（a）]，致使屈曲问题变得复杂起来。经过对非弹性屈曲在理论方面的长期研究，得出轴心压杆在非弹性阶段时的临界应力，用切线模量理论计算比较接近实际[见图4.8（c）]，即

图4.8　切线模量理论

（a）σ—ε曲线；（b）σ—Et曲线；（c）σcr—λ曲线

相应的切线模量临界应力为

4.3.1.2　实际压杆(即工程压杆)的屈曲

在实际结构中，上述理想的轴心压杆并不存在，由于种种原因，经常出现一些不利因素，如初弯曲、初偏心、残余应力等缺陷，在不同程度上使压杆的承载能力降低。在设计这种构件时必须充分予以考虑。

（1）构件的初弯曲和荷载初偏心的影响。图4.9示有初弯曲和初偏心的轴心受压构件的临界平衡状态。图4.10示有临界力和杆中挠度之间的关系。

图4.9　有初弯曲和初偏心的轴压杆件

由图可见，初弯曲和初偏心对轴心受压杆件工作的影响是类似的。这些影响可归纳为三点:①在压力一开始作用时，杆件就产生挠曲，并随着荷载的增加而增大，开始时增长较慢，而后迅速增长，当压力趋近欧拉力时，挠度无限增大；②初挠度y0或初偏心e0越大时，在相同的压力作用下，杆件的挠度也越大；③不论y0或e0多小，杆件的临界力N总小于欧拉力Ncr。

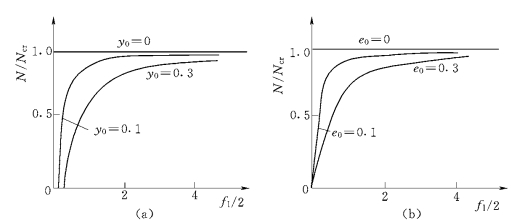
图4.10　初弯曲和初偏心的影响

（2）残余应力的影响。

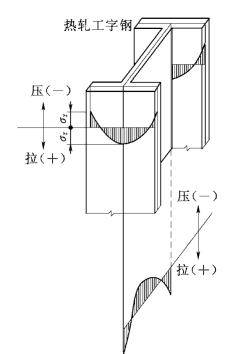
图4.11　残余应力自相平衡

1）残余应力的产生及分布。残余应力的产生原因有:①焊接；②热轧型钢的不均匀冷却；③冷加工；④火焰切割等。其中焊接残余应力数值最大，通常可达到或接近钢材的屈服强度fy。残余应力是一种初应力，即构件受荷载前，截面上就已存在的应力。在一个截面上，残余应力具有自相平衡的特点见图4.11。

杆件中残余应力的产生、分布及其大小，与杆件的截面现状、尺寸，加工方法和加工过程有密切关系，而与材料的屈服点关系不大。图4.12为热轧宽翼缘工字钢截面[图4.12（a）]、焊接工字形截面[图4.12（b）]和焊接箱形截面[图4.12（c）]的残余应力分布（当板厚较大时，残余应力在板厚方向有变化，图中所示为沿板厚方向的平均值）。对图4.12（a）来说，由于在热轧冷却过程中，翼缘两端单位面积的暴露面积比翼缘与腹板相交处大，因此冷却较快；同样，腹板中间部分也比腹板两端相交处较快冷却，后冷却的区域就会受到较早冷却部分的约束，因而板在相交处产生拉应力。相反，在早冷却部分截面上则产生压应力。

图4.12　构件残余应力的分布(www.xing528.com)

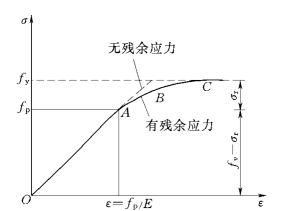
图4.13　残余应力对轴心受压短柱平均应力—应变曲线的影响

2）残余应力对短柱应力—应变曲线的影响。残余应力对应力—应变曲线的影响通常由短柱压缩试验测定（见图4.13）。所谓短柱就是取一柱段，其长细比不大于10，不致在受压时发生屈曲破坏，又能足以保证其中部截面反映实际的残余应力。

将有残余应力的短柱与经退火热处理消除了残余应力的短柱试验的σ—ε曲线对比可知，残余应力对短柱的σ—ε曲线的影响是:降低了构件的比例极限；当外荷载引起的应力超过比例极限后，残余应力使构件的平均应力—应变曲线变成非线性关系，同时减小了截面的有效面积和有效惯性矩，从而降低了构件的稳定承载力。

3）残余应力对构件稳定承载力的影响。残余应力对构件的强度承载力并无影响，因它本身自相平衡。但对稳定承载力是有影响的，因为残余应力的压应力部分将使该部分截面提早发展塑性。因此，将使轴心受压构件达临界状态时，截面由变形模量不同的两部分组成，屈服区的弹性模量E＝0，而弹性区的模量仍为E，已屈服的塑性区，不能继续有效地承载，只有弹性区才能继续有效承载。因此，只能按弹性区截面的有效截面惯性矩Ie来计算其临界力，即

相应临界应力为

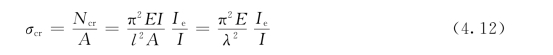
式（4.12）表明，考虑残余应力影响时，弹塑性屈曲的临界应力为弹性欧拉临界应力乘以小于1的折减系数Ie/I。比值Ie/I取决于构件截面形状尺寸、残余应力的分布和大小，以及构件屈曲时的弯曲方向。EIe/I称为有效弹性模量或换算切线模量Et。

图4.14（a）代表H形钢或翼缘为轧制边的焊接工字形截面，由于残余应力的影响，翼缘四角为塑性区，故对x—x轴（强轴）屈曲时

式中　Ae——翼缘的弹性区面积；

A——总面积；

η——翼缘的弹性区面积Ae与总面积A，即。

对y—y轴（弱轴）屈曲时

由于式（4.13）和式（4.14）中η＜1，故Ety≪Etx。由此可见，残余应力的不利影响，对绕弱轴屈曲时比绕强轴屈曲时严重得多。原因是远离弱轴的部分是残余压应力最大的部分，而远离强轴的部分则兼有残余压应力和残余拉应力。

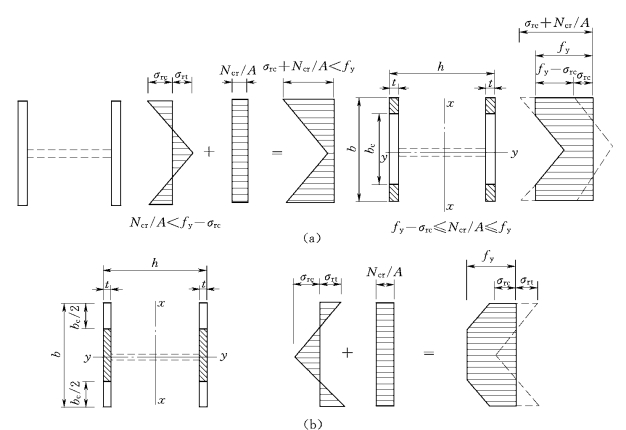
图4.14　残余应力对轴心受压杆稳定的影响

（a）H型钢或翼缘为轧制边；（b）翼缘为火焰切割边

若残余应力分布为另一种情况，如图4.14（b）所示用火焰切割钢板焊接而成的工字形截面。由于残余应力的影响，翼缘中部为塑性区。同样可以证明，对x—x轴（强轴）屈曲时，Etx与式（4.13）相同，但对y—y轴（弱轴）屈曲时

式（4.15）数值显然比式（4.14）大，由此可见，用火焰切割钢板焊接而成的工字形截面，由于在远离弱轴翼缘两端具有使其推迟发展塑性的残余拉应力，因而对弱轴屈曲时临界应力比用轧制边的工字形截面的高。而对绕强轴屈曲时残余应力的不利影响，两种截面是相同的。

4.3.1.3　实际轴心受压构件整体稳定的计算

（1）计算公式。根据轴心受压构件的稳定承载力Nu，考虑抗力分项系数γR后，即可得《钢结构设计规范》规定的计算其整体稳定性的公式

或

式中　σcr——构件的极值点失稳临界应力；

γR——抗力分项系数；

N——轴心压力设计值；

A——构件的毛截面面积；

f——钢材的抗压强度设计值，按附表1.1采用；

φ——轴心受压构件的整体稳定系数，可根据表4.4和表4.5的截面分类和构件的长细比或换算长细比（按），按附表4.1～附表4.4查出。

（2）柱子曲线和稳定系数φ的确定。实际轴心受压构件受残余应力、初弯曲、初偏心的影响，且影响程度还因截面形状、尺寸和屈曲方向而不同，每个实际构件都有各自的柱子曲线，因此它的柱子曲线分布很离散。《钢结构设计规范》制定时，根据我国较常用的截面形式，按不同尺寸、不同加工条件及相应的残余应力图，经过计算和实验研究，共算出96条纵坐标用φ＝σu/Afy、横坐标用长细比的柱子曲线，图4.15中的两条虚线表示这些曲线的分布带范围。这个分布带的上、下限相差较大，特别是中等长细比的常用情况相差尤其显著。因此，若用一条曲线来代表，显然是不合理的。规范将这些曲线分成四组，也就是将分布带分成四个窄带，取每组的平均值（50%的分位值）曲线作为该组代表曲线，给出a、b、c、d四条柱子曲线，如图4.15所示。在常用范围（λ＝40～120），a曲线的φ值最高（比b类高4%～15%），c曲线的则较低（比b类的低7%～13%），而d曲线的最低，它主要用于t＞40mm厚板中的某些截面。

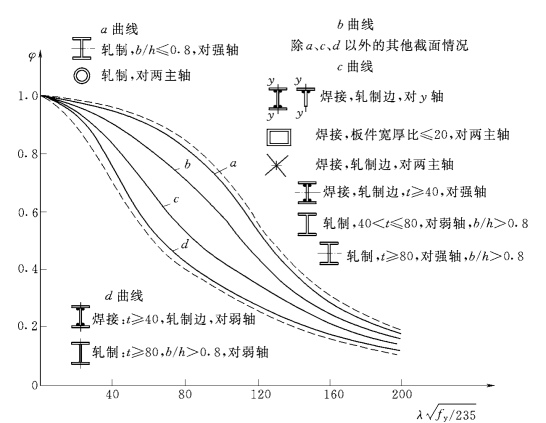
图4.15　柱子曲线

对应于a、b、c、d四条曲线的轴心受压构件截面分类见表4.4和表4.5，大部分的截面形式属于b类。

设计轴心压杆时，除应满足式（4.16）的要求外，还应使构件的长细比λ不超过规范规定的长细比限值[λ]，即

式中　[λ]——受压构件的长细比限值，由表4.6查得。

表4.4　轴心受压构件的截面分类（板厚t＜40mm）

表4.5　轴心受压构件的截面分类（板厚t≥40mm）

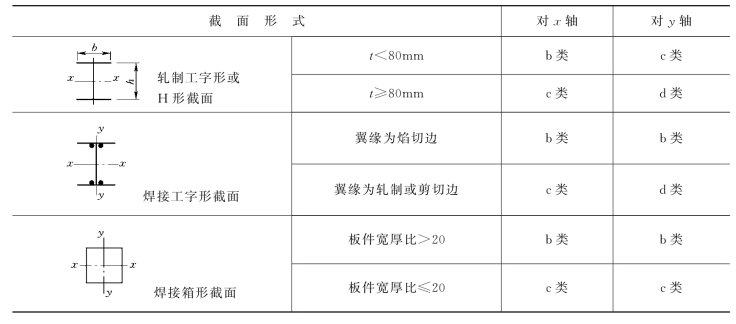
表4.6　受压构件的长细比限值[λ]

注　在桁架（包括空间桁架）结构中的角钢受压腹杆，当其内力等于或小于承载能力的50%时，可取[λ]＝200。

构件长细比λ应按照下列规定确定

式中　l0x、l0y——构件对主轴x轴、y轴的计算长度；

ix、iy——构件毛截面对主轴x轴、y轴的回转半径。