2.2.1.1 抗拉力学性能
Q235低碳钢标准件在常温、静载的情况下,用拉伸机单向拉伸,可测得应力—应变曲线(图2.1),随着荷载与应力的增加,看到钢材从开始受力到拉断全部过程可分为四个阶段,每个阶段表现出不同的性质。概括起来有下列性能:
(1)弹性性能。图2.1中σ~ε曲线的OP段为直线变化,钢材完全属于弹性变形,当外力撤消后,变形完全消失,此阶段称为弹性阶段。此时的应力与应变的关系用材料的弹性模量定义,即σ=Eε,E=tanα,符合虎克定理,P点对应的应力fP称为比例极限(proportional limit)。
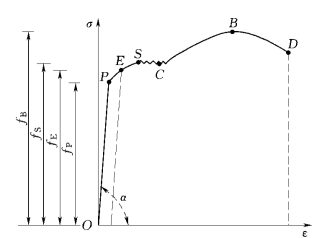
图2.1 钢材一次单向拉伸σ~ε曲线
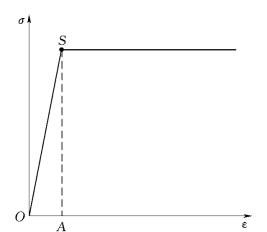
图2.2 理想弹性、塑性体σ~ε曲线
PE段为曲线变化的,材料仍然属于弹性变形,叫做非线性弹性阶段,当外力撤消后,变形也完全消失。此时的弹性模量用切线模量定义,Et=dσ/dε。此段E点的应力fe称弹性极限。比例极限与弹性极限虽然意义不同,但在σ~ε曲线上二者非常接近,在工程上一般不加严格区分,统称为弹性极限。
(2)塑性性能。当应力超过弹性极限fe达到某一数值时,σ~ε曲线上出现ES阶段,表现为非弹性变形阶段,称塑性变形阶段,当外力撤消后,留下永久的残余变形。S点对应的应力称上屈服点。
随着荷载的增加,σ~ε曲线上出现SC阶段,此时变形进入塑性流动阶段,曲线波动较大,逐渐趋于平稳,曲线上出现近似水平的锯齿状线段,属于典型的塑性变形,C点称为下屈服点。试验结果表明,材料的上屈服点S点受外界因素(加荷速度、试件形状、试件对中的准确性)影响较大,其数值不稳定。而下屈服点不受上述外界因素的影响,所以将下屈服点C点所对应的应力fy称为屈服强度,也称为屈服点(yield point或yield strength),用fy来表示。因为钢结构工作状态不允许出现较大的变形,它的破坏定义为塑性变形破坏,故将屈服强度作为钢筋设计强度标准的依据。
(3)强化性能。经过屈服阶段,材料又恢复了抵抗变形的能力,即进入CB阶段。这是由于材料在滑移到一定程度,晶格间因形状的改变产生了新的阻力而致。此时材料又重新获得了抵抗外力的能力,此阶段称为强化阶段,最高点B点对应的应力称抗拉强度(tensile strength)fu。抗拉强度是材料发生拉伸断裂的依据。不作为钢结构设计的依据。强化阶段的变形绝大部分为塑性变形,此时整个试件的横向尺寸明显减小。
(4)局部变形性能。过了强化阶段,进入BD阶段,此时试件局部尺寸急剧变细,出现了缩颈现象,抗拉能力下降,σ~ε曲线出现下降趋势,直到D点处拉断。称这一阶段为局部变形阶段。
2.2.1.2 冷作硬化性能
如图2.4所示,当应力达到F点时,然后逐渐卸除拉力,应力与应变关系沿着FF′直线下降到F′点,直线FF′与OP段近似平行,此现象称卸载定律。F′G段为弹性变形,OF′是残余下来的塑性变形段。在卸载后的短期内再加荷载,应力与应变关系沿着FF′直线上升到F点,然后继续沿着σ~ε曲线变化,这表明第二次加载后,变形没有屈服流动阶段,材料的比例极限(弹性极限)提高了,塑性变形和延伸率降低了。这种现象称为冷作硬化。
在工程上常常利用冷作硬化来提高材料的强度,如预制楼板中的预应力冷拔钢筋等。
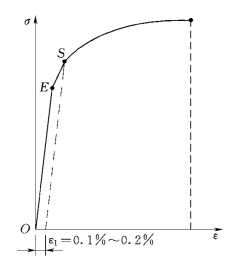
图2.3 高强度钢的σ~ε曲线(https://www.xing528.com)

图2.4 钢材单向受压σ~ε曲线
图2.2是理想的弹性塑性体的应力与应变曲线。由于低碳钢和低合金钢的流幅相当长,当应力达到屈服点后出现塑性流动时,钢材由理想的弹性体变为近似于理想的塑性体。在此阶段,应力与应变曲线基本上相同于弹性塑性体的应力与应变曲线。因此,这类钢材可认为是理想的弹性塑性体。
高强度钢材没有明显的屈服点和屈服台阶。这类钢材的屈服条件是根据实验分析结果而人为规定的,故称为条件屈服点(或屈服强度)。条件屈服点是以卸荷后试件中残余应变为0.2%所对应的应力定义的,用f0.2表示,见图2.3。由于这类钢材不具有明显的塑性平台,设计中不宜利用它的塑性。
超过屈服台阶,材料出现应变硬化,如图2.1所示曲线上升,直至曲线最高处的B点,这点的应力fu称为抗拉强度或极限强度。当应力达到B点时,试件发生颈缩现象,至D点而断裂。当以屈服点的应力fy作为强度限值时,抗拉强度fu成为材料的强度储备。
2.2.1.3 抗压力学性能
3号低碳钢试件在常温的情况下,用压力机单向压缩时,σ~ε曲线如图2.4所示。试验表明,压缩时的弹性模量、比例极限、屈服极限等均与拉伸时基本相同,即此阶段拉伸与压缩曲线基本重合。但在屈服阶段以后,试件压扁,横截面变大,σ~ε曲线趋于直线上升,无法测得压缩时的强度极限。
一般对于塑性材料只作拉伸试验,受压的力学性能指标均采用拉伸时的力学性能指标进行计算的。
2.2.1.4 抗剪力学性能
钢材单元体在纯剪切应力状态下,正六面体将变成平行六面体,剪应力τ与剪应变γ存在着一定的线性与非线性关系。取薄壁圆筒作试件进行纯剪切试验,可得到剪应力与剪应变τ—γ曲线如图2.5所示。此图与受拉试验图很相似。
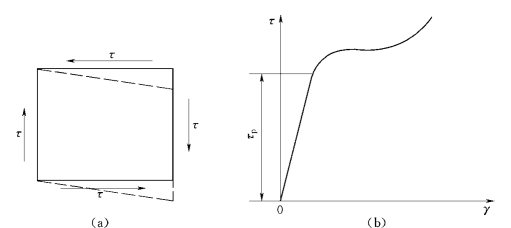
图2.5 剪应力与剪应变关系τ~γ曲线
当剪应力不超过剪切比例极限τP时,剪应力与剪应变存在着线性比例关系,即符合剪切虎克定理:τ=Gγ;式中G为剪变模量。总之,剪变模量G、比例极限τP、屈服强度τy及抗剪强度均较抗拉时为低。
钢材和钢铸件的弹性模量E、剪变模量G、线性膨胀系数α和质量密度ρ见表2.1。
表2.1 钢材和钢铸件的物理性能指标

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




