多尺度分析：混凝土随机损伤本构理论的模拟研究

在此背景下，本书引入不规则有限元网格考虑微观非均匀性对于宏观裂缝扩展的影响，建立了非规则内聚单元模型考虑动力加载条件下微裂缝的产生和演化过程，初步进行了混凝土材料的动力损伤细观数值模拟研究。

5.2.3.1　分析模型

非规则内聚单元模型的建立过程如图5-7所示：考虑平面断裂问题，首先确定平面固体所在区域；其后在固体的边界上和内部随机生成代表性点集；再基于生成的随机代表性点集，对固体所在区域进行Delauney三角分割；最后基于平面三角分割生成体积单元和内聚单元。

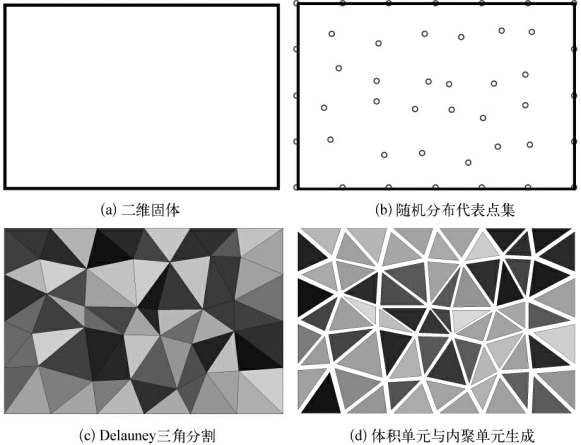
图5-7　非规则内聚单元模型的生成

采用非规则内聚单元模型模拟图5-8所示的二维动态断裂问题。数值试件的几何尺寸为：l=4.5m，h=1.5m，a=0.21m。固体的材料参数取为：E=30GPa，ν=0.2，ρ=2 400kg／m3。由此计算可得固体的压缩波速c1=3 228m／s，剪切波速c2=2 282m／s，瑞雷波速cR=2 079m／s。采用线性内聚裂缝模型描述内聚单元的性质，最大内聚应力ft=32MPa，断裂能2Γ0=100m／s。边界条件为：下边界固定y方向自由度；上边界施加恒定速率ν驱动内部裂纹的扩展。为了尽量精细地模拟混凝土的动态断裂行为，我们建立了非常精细的有限元模型，单元数量超过30万：其中体积单元数量为13.5万，而内聚单元的数量为20万。采用显式积分方法并引入并行计算策略进行数值模拟。

图5-8　二维动态断裂模型

5.2.3.2　裂纹扩展模式与端部应力场

数值模拟所得微观裂纹扩展模式如图5-9所示。裂缝自预留开口端部开始扩展，不同加载速率下裂纹扩展的模式具有很大的区别。对于加载速率比较低的拟静态加载，裂纹倾向于沿着一个面扩展，虽然也产生了一些微观分叉，但是整体而言还位于一个断裂面上，这与经典断裂力学的假设是一致的。对于加载速率较高的动态加载，裂纹扩展过程中产生了大量的分叉，同时这些分叉具有某些递归自相似特性。这就使得动态加载条件下，微观的裂纹不再是一个断裂面，而产生了一个裂缝群，可以预见，裂缝群的性质与单一裂缝面的性质有着本质的不同，所以此时断裂动力学不再适用。另一方面，本书基于非规则内聚单元模型模拟所得的裂纹扩展模式也与分子动力学模拟结果有一些不同。根据Abraham等人［195］的分析，动态裂纹扩展的断裂面的变化过程为“平滑（smooth）→粗糙（rough）→曲折（zigzag）”，而本书结果所体现出的动态裂纹的典型特点为自相似分叉。计算得到的随机分叉裂缝与实际的岩石或者混凝土裂缝具有很好的相似性［201］。

图5-9　裂纹扩展模式

下面考察裂纹端部场（图5-10）。可见拟静态断裂的裂纹端部场（图5-10a）与断裂力学给出的裂纹端部场的应力分布具有很好的一致性，这从一个侧面验证了本书模型的正确性。而动态断裂的裂纹端部场与静态裂纹有着本质的区别，不能用单条裂纹得到的裂缝端部场的解描述。裂纹的分叉减弱了裂纹端部的应力集中，但是加剧了应力的波动，波动的裂纹端部应力场又进一步加剧了裂纹扩展的分叉。同时，由于本书采用了随机分布点集生成计算模型，所以局部裂纹扩展的方向具有随机性，而裂纹的随机扩展进一步加剧了裂纹端部应力场的复杂性。

图5-10　裂纹端部场（σy）

5.2.3.3　率相关效应的分析与探讨

动力加载条件下裂纹的扩展速率是动力断裂的重要指标，我们通过数值模拟结果研究了裂纹扩展速率随着其扩展长度的变化。由于动态加载条件下，裂纹不再是一个断裂面而是一个分叉的裂缝群，所以可能会有多个裂纹尖端同时扩展，所以这里先将裂缝群的端部定义为最前端的裂缝端部，裂缝群的长度和扩展速率均由最前端的裂纹端部给出。定义名义应变率=ν／h为加载速率与试件高度的比值，图5-11给出了不同加载速率下的裂纹扩展速率沿着裂纹长度的演化曲线。可见随着加载速率的增长，裂纹的扩展速率表现出了很强的波动性，其变化已经不再是连续的光滑函数。另一方面，如果对不同加载速率下的裂纹扩展速率曲线做局部平均而求得平均裂纹演化速率，那么可以看出加载速率对裂纹动态扩展速率的影响非常有限，裂纹扩展达到上限速率ccrit之后就不再增加。本书数值模拟得到的裂纹扩展的上限速率大约为0.75倍的瑞雷波速，即ccrit≈0.75cR，小于断裂动力学所预测的一倍瑞雷波速。当裂纹的扩展达到极限速率后，裂纹就以分叉的形式耗散多余的能量，而保持整体扩展的速率基本不变，因此，在相同外加应变条件下，高速加载所得的裂纹扩展要滞后于低速加载，从而使得其刚度和平均应力都有提高，本书认为：这恰恰是脆性固体材料产生动力强化的物理原因。

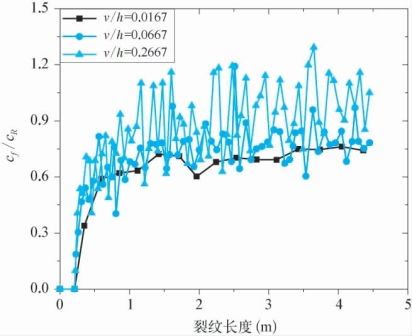
图5-11　裂纹扩展速率

下面进一步从能量的角度考察动力断裂系统。首先有能量平衡表达式如下

(www.xing528.com)

其中，U为总能量；WL为外力功；UE为应变能；US为形成新的断裂面所需要的表面能；UK是系统的动能。

如果不考虑动能项，式（5-43）右端的前三项描述了静态断裂的能量平衡，与Griffith最初给出的表达式［202］一致。后来，Mott［203］引入了动能项UK考虑动态断裂系统。但是由于当时理论与计算水平的限制，Mott只能类比静态断裂应力场的某些结果并结合量纲分析假定动能的表达形式，最终得到了裂纹扩展极限速度的半经验表达式。

图5-12　动态断裂的能量演化（ε·=0.066 7s-1）

图5-13　动态断裂的断裂能释放率演化

本书根据数值模拟的结果，得到了能量各个分项的演化曲线如图5-12所示。可以看出，加载的早期外力功主要转化为系统的应变能；随着应变能的增加裂缝的扩展在某个极限状态激活，微裂纹的扩展消耗了越来越多的外力做功，而系统的动能主要由断裂面的回弹引起；应变能的增加越来越缓慢并最终进入下降段直至破坏。这里的数值分析结果严格满足能量平衡条件即U=0，这也验证了本书数值模拟的正确性。

总能量U对裂纹长度c求微分，有

将式（5-43）代入上式，整理得

此处静态断裂能释放率

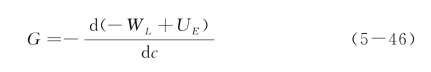
断裂表面能

那么动态断裂能释放率

对于静态断裂而言，裂纹只形成两个光滑的断裂面，可知其断裂表面能为常数，其取值由材料本身决定，即

同时由裂纹端部场计算得到的断裂能释放率G可以作为断裂开展的驱动力。对于动态断裂而言，结果则完全不同。事实上，在动态加载条件下，由于裂纹的持续分叉，使得不同时刻裂纹断裂面的个数不同，并且随着加载速率的变化而变化，所以动态断裂表面能就不再是常数，而是与加载速率有着密切的关系（图5-13）。因此不能够直接采用动态断裂能释放率Gd作为动态断裂的驱动力。同时，由于裂纹扩展速率的波动性，使得断裂能释放率的演化也呈现出波动性，并且波动的幅度也与加载速率密切相关。