混凝土随机损伤本构理论研究中的内聚单元方法

在上一章中我们已经详细介绍了内聚单元方法的基本思路和理论。1999年，Xu和Needleman［166］最早采用内聚单元方法模拟固体的动态断裂问题。在这类模型中，首先对固体进行有限元离散，划分得到的有限元称为体积单元（volumetric element）。与传统有限元不同的是，体积单元之间并没有共用的节点，而是相互独立的，在邻近的体积单元之间插入内聚单元（cohesive element）作为体积单元的连接，同时作为裂缝可能的路径（图5-6）。

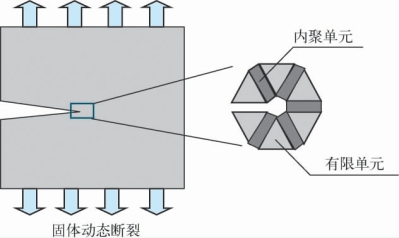
图5-6　动态断裂的内聚单元模型(www.xing528.com)

基于内聚单元模型，Xu和Needleman在数值模拟的基础上，得到了关于动力断裂的一些重要结论：第一，动力加载过程中，裂缝扩展速度会增长至一个平台而不继续增长，对于各向异性材料，这个平台大约为瑞雷波速的90%，而对于各向同性材料，平台大约为瑞雷波速的50%；第二，在到达了裂缝扩展速率平台之后，裂缝开始分叉，并且扩展速度出现很强的波动；第三，裂缝动态扩张条件下，其断裂能和断裂韧性不再是常数，甚至不再是连续函数。显然，这样的三点结论均被12年后Buehler和Gao所进行的分子动力学模拟研究［200］所验证，从而说明了上述细观数值模拟方法的有效性。

内聚裂缝模型虽然可以在适当的空间和时间尺度范围内给出材料动态断裂的模拟结果，但是其本身仍然存在某些问题，如：内聚力与裂缝张开位移的关系很难直接测量和确定。同时，在既有研究中，内聚裂缝模型大都基于规则网格，没有考虑不规则网格对于模拟结果的影响。