首先考虑最简单的情形,即弹性固体中包含静态的裂缝,但是承受动力荷载的情形。显然这类问题可以用弹性波动方程描述[182]。这里考虑平面波动方程,引入Lame势函数φ(x,y,t)与φ(x,y,t),有
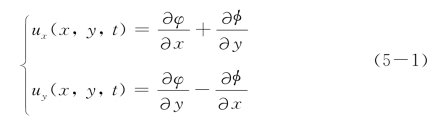
由应变位移关系与胡克定律,可以求得应力的表达式
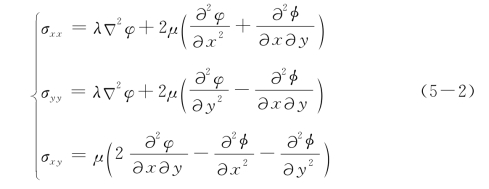
Lame势函数满足波动方程
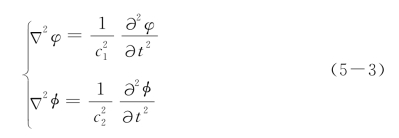
其中
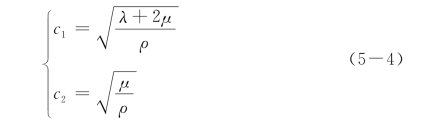
分别为固体的压缩波速和剪切波速。而λ与μ为Lame常数,ρ为固体密度。对于反平面问题,以位移uz作为基本未知量,应力分量为

uz满足波动方程

Sih等人[183]得到了平面I、II、III型裂缝在无穷远处承受冲击响应的解析解。范天佑[181]将其求解的基本过程归结为,首先用拉普拉斯变换消去时间变量,继而用傅立叶变换消去一个空间变量,使得偏微分方程转化为常微分方程,求解常微分方程并用边界条件确定未知函数,就得到最终的解。
考虑无限平面内包含一条裂缝,如图5-1所示。裂纹全长L=2a,半长l=a;坐标系建立在裂纹中心,x轴与裂纹平行。裂缝上下表面承受冲击荷载作用,根据作用方式的不同,分为I、II和III型断裂问题,下面将分别给出各型断裂的解和主要结论。
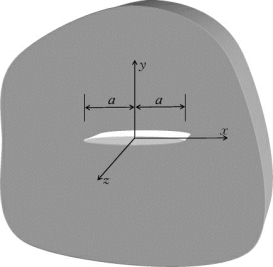
图5-1 无限平面中的贯通裂缝
对于I型(张开型)断裂问题,由于对称性,可以只考虑上半平面,其对应的边界条件为
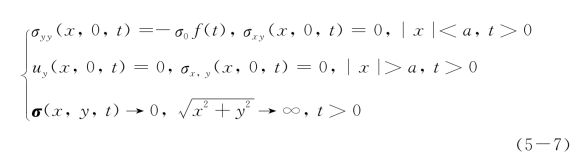
其中,σ0为动力加载的幅值;f(·)为动力加载的时程函数。
假定物体初始处于静止状态,对应初始条件为
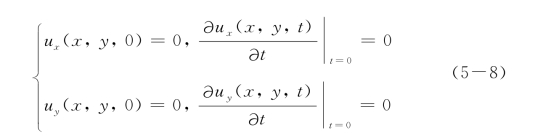
利用拉普拉斯变换和傅立叶变换[181],可得应力强度因子的解
![]()
![]() 为静态应力强度因子。(https://www.xing528.com)
为静态应力强度因子。(https://www.xing528.com)
动力强度因子的时程函数可表示为拉普拉斯逆变换如下
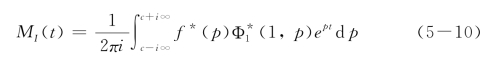
其中c为材料的特征波速,此处可取为面波波速。函数
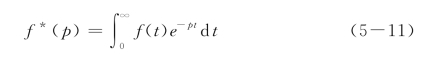
为f(t)的拉普拉斯变换。
函数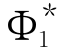 (ξ,p)可由下面积分方程求出
(ξ,p)可由下面积分方程求出
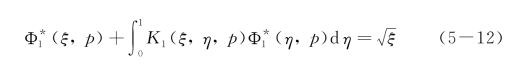
积分方程的核函数K1(ξ,η,p)为
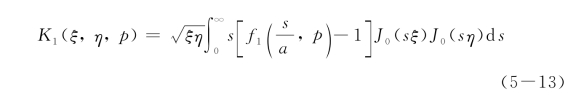
其中J0(·)为0阶贝塞尔函数,而函数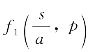 即f1(s,p),表示为
即f1(s,p),表示为
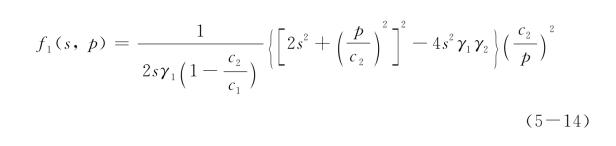
其中γ1与γ2为
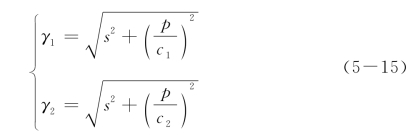
对于II型与III型断裂,需要将边界条件中裂缝上下表面的作用项转化为
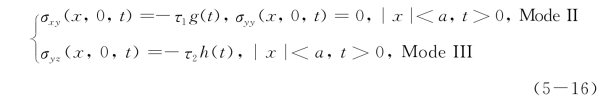
采用与I型断裂类似的处理过程,可得其表达式与I型断裂基本一致,只有式(5-13)中f(·)函数的表达式不同,对于II、III型断裂,分别为

采用数值方法计算上述一系列方程,可得动态应力强度因子。
图5-2 Heaviside函数
考虑最简单的情形,取动力加载时程函数为Heaviside函数H(t)(图5-2),其拉普拉斯变换为1/p,代入上面公式进行计算,最终可得动态应力强度因子。Heaviside型荷载作用下I、II与III型断裂的应力强度因子计算结果如图5-3。由这一数值结果可以看出,动态荷载作用下,裂缝端部的应力强度因子呈现出复杂的变化过程。由于Heaviside函数后面是平稳段,所得动态应力强度因子也平稳地趋于静态应力强度因子。但是由于初始的冲击作用,动态应力强度因子的初始上升段可使其超过静态应力强度因子的数值。有关数值分析的结果表明[181],对于有限边界动态断裂问题,由于边界对波动的反射,使得其应力强度因子呈现出更加复杂的变化过程,其数值可能上升到静态应力强度因子的5—10倍。
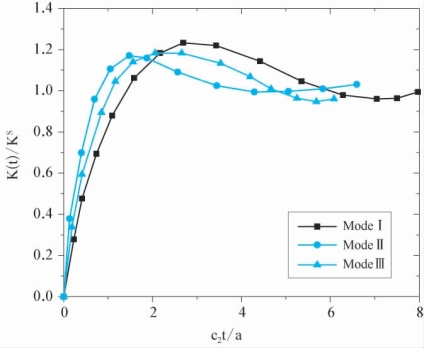
图5-3 Heaviside型荷载作用下动态强度因子
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




