混凝土随机损伤本构理论研究中的单元分析与尺寸效应

考虑如图4-7所示细观单元分析模型。固体处于二维受力状态，其中包含一条裂缝自中心开始扩展。数值模拟中采用内聚裂纹模型模拟裂纹的扩展，并且取线性分布内聚应力分布模型式（4-123），同时不考虑裂纹以外固体的非线性。

图4-7　单元体分析模型

基于前面章节讨论的细观数值算法，首先模拟单元行为，可得不同加载阶段的应力-应变场。图4-8给出了不同阶段的竖向应力场的分布。从中可以明显地看出微裂缝的产生和扩展及其对固体内应力场的影响。基于计算得到的不同阶段的应力-应变场，利用多尺度能量传递定理，可以得到Helmholtz自由能势的演化，进而利用多尺度损伤表示理论得到损伤的演化，计算所得均匀化状态量的演化结果如图4-9。

图4-8　单元体不同加载阶段竖向应力云图

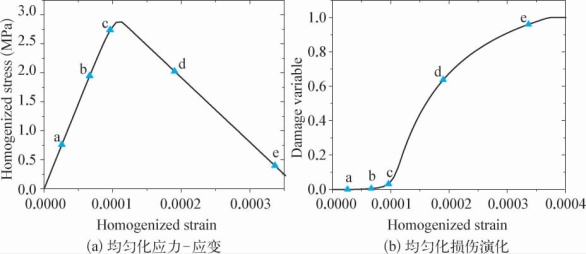
图4-9　均匀化状态量

（图中a、b、c、d和e点与图4-8中5个应力状态一一对应）

上述计算过程中，也可以灵活地考虑某些技巧。如果细观数值分析是基于加强函数方法进行的，那么能量积分表达式需要基于式（4-68），分别考虑弹性基体内的体积分和沿着裂缝表面的面积分。如果细观数值分析采用界面单元方法，此时裂纹已经“弱化”到界面单元内，那么既可以根据式（4-68）分别计算体积分和面积分，也可以直接将界面单元内的积分直接考虑为体积分，同基体的体积分一同进行，此时需要借助非线性材料的多尺度能量传递公式（4-78）计算自由能的演化，同时不必单独考虑沿着裂纹面的面积分项。作者尝试了不同的方法，发现上述方法得到的能量及损伤演化都非常接近，但是直接利用非线性积分公式能够减少能量积分的计算量。

下面研究多尺度损伤演化的尺寸效应（size effect）。首先引入无量纲尺度参数λ，定义为细观特征尺度lmic与宏观特征尺度lmac之比，有

(www.xing528.com)

本书中细观特征尺度取单元的长度l，宏观特征尺度取梁的截面高度h，于是无量纲参数的表达式化为

变化单元的尺寸，进行多组数值试验，得到的均匀化状态量的演化曲线如图4-10所示。由图中结果可以看出，单元体的尺度对于均匀化状态量的演化有着很大的影响。这类尺寸效应产生的实质原因在于其中微裂缝所引入的内在材料尺度。实际上，对于不同尺度的单元体，其裂缝的性质是一致的，描述内聚裂缝的参数ft和Gc并不会随着单元体尺度的变化而变化。然而，由于单元体所储存的应变能随着尺度的平方增长，但是其中裂缝扩展所耗散的能量却随着单元体的尺度线性增长，因此，随着单元体的增大，裂纹扩展耗散的能量中单元体内部应变能释放所占据的比例越来越大，而外力做功则越来越小。前面已经述及材料的均匀化性能是其外部表现，与外力做功直接相关。于是随着单元体的增大，均匀化应力-应变曲线逐渐缩小，最后甚至出现了反向跳回（snap-back），即弹性能释放率高于裂缝开展的能量耗散率，外力必须做负功才能使整个系统能量平衡。图4-10a中就很好地体现了这种趋势。同时图4-10b中损伤演化也表现出了强烈的尺寸效应，随着单元体尺寸的增加，损伤演化趋前并且趋快。

图4-10　均匀化状态量

均匀化状态量的尺度依赖性具有很强的规律性，如图4-11所示。对于峰值强度的尺度效应，可以用经典的尺寸效应公式加以考虑。Bazant［91］引入了如下半经验公式考虑峰值强度与试件尺寸之间的依赖性，有

图4-11　网格依赖性

其中σN为名义强度，具有尺度相关性，l为试件的尺寸；B与l0为与尺度效应有关的材料参数。由尺寸效应的公式（4-127）可以看出，当试件的尺度l→0时，名义强度趋近于实际强度，试件趋于强度破坏；当试件尺度l→∞时，名义强度与成正比，这与线弹性断裂力学的结论一致。强度破坏与线弹性断裂破坏的过渡部分，是非线性断裂力学的控制区域，使得不同的破坏模式之间实现了平滑的过渡。图4-11a中本书数值结果的尺度依赖性与Bazant经典尺寸效应的结果非常吻合。将试件均匀化应力峰值所对应的均匀化应变定义为均匀化峰值应变εt，将试件均匀化应力降为0时所对应的均匀化应变定义为均匀化断裂应变εu。将二者之差εu-εt作为应变指标考察均匀化应变的尺度依赖性，结果如图4-11b所示。由于目前还没有成熟的描述应变尺寸效应的公式，所以本书只简单地取对数坐标系中的线性拟合公式描述应变的尺度依赖性。