考虑包含界面的固体Ω(图4-3),界面S代表位移场的不连续面,物理上可以是裂缝或者剪切带等厚度可以忽略的强非线性区。可采用界面S将整体区域Ω隔离成两部分,即Ω+和Ω-,分别建立固体问题的泛函,有

图4-3 包含界面的固体

上面两式相加,有
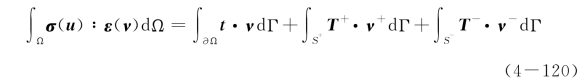
考虑到界面层的平衡条件,有T=T+=-T-,那么上式化为

其中w(ν)=ν--ν+。
在能够求解上述系统之前,需要先确定界面层应力T的表达式。如果将界面层看作固体内部的裂缝,那么上述界面层的内应力可以由内聚裂缝模型(cohesive crack model)确定。
内聚裂缝模型的基本思路如图4-4所示,根据弹性断裂力学的解,其裂纹端部的应力趋于无穷,这在物理上是不可能的,所以裂缝的端部介于裂纹张开区域和线弹性固体区域之间,必然存在一个非线性区段,区段内的材料因为局部的损伤和断裂进入非线性(图4-4a),进而使得应力降低到物理上的合理数值。为了简化,分析中将物理裂纹延伸到弹性区域边缘,称为数学裂纹(图4-4b),然后将非线性区域内材料的内聚应力(cohesive stress)以外力的形式作用到裂缝端部区,就得到了内聚裂缝模型(cohesive crack model)。
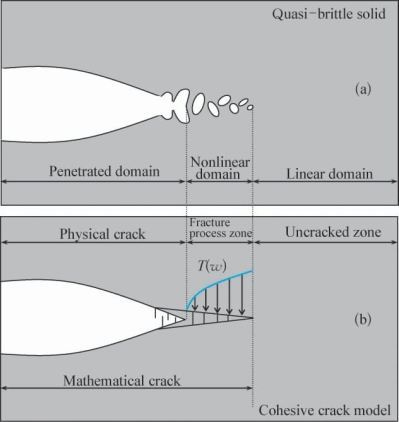
图4-4 内聚裂缝模型
(a)脆性固体的裂缝尖端;(b)内聚裂缝模型(https://www.xing528.com)
内聚裂缝模型中,内聚应力一般考虑为裂缝张开位移的函数
![]()
其中裂缝张开位移w(u)=u--u+。
最早研究内聚裂缝模型是Dugdale[163]。在最初的工作中,Dugdale试图利用材料的非线性本构关系确定内聚应力的分布形式。对于金属材料,满足理想弹塑性假定,那么内聚应力沿着断裂作用区(fracture process zone)的分布形式为常数。Dugdale据此解出了等效裂纹长度与等效应力强度因子的表达式,此工作在以后的几十年间被广泛地引用。之后,Barenblatt[164]从数学角度系统阐述了内聚裂缝模型的理论和应用,并把内聚应力沿着断裂作用区的分布形式当作内禀的材料性质以唯象的形式加以考虑。后来,Hillerborg[165]将断裂能的概念引入到内聚裂缝模型中,并针对混凝土等脆性材料提出了几类有用的内聚应力的分布函数。对于混凝土等材料,其内聚应力的分布一般取线性分布形式,有
![]()
此处f=T·n和w=w·n分别为法向内聚应力和裂缝张开位移;fu为材料的抗拉强度。
材料的内聚性断裂能定义为f-w曲线下面包围的面积,对于线性模型,有![]() 。
。
在式(4-121)中考虑内聚裂缝模型,有
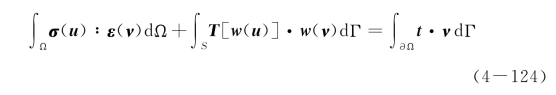
上式左边两项具有类似的能量对偶形式,并具有统一的位移场u和试函数场v,同时其积分区域可以划分到不重合的几个部分,那么可以考虑统一划分网格计算,对于固体部分的网格,采用第一项积分计算,对于界面部分的网格,采用第二项积分计算,两类网格可以直接组装到一起构成整体刚度矩阵,这就得到了内聚单元方法(cohesive element method),如图4-5所示。基于内聚单元方法,Xu and Needleman[166]对固体中裂纹的快速动态扩展进行了数值模拟,为了考虑任意方向的裂缝扩展和分叉,Xu and Needleman在有限元网格之中所有相邻的有限元之间均设置了内聚单元。后来,Camacho and Ortiz[167]用类似的方法模拟了固体在冲击作用下的裂缝开展和破碎。上面两个工作使得人们意识到内聚单元的实用价值。由于内聚单元直接基于位移构造,所以单元计算中不需要利用位移场的梯度求解应变,这就大大提高了数值模拟的稳定性,更使得这类方法适用于多裂缝、裂纹分叉、固体破碎等强非线性问题,同时这类方法能够与传统的有限元方法很好地结合,其效率也非常高。当然,在使用内聚单元求解裂缝扩展问题的过程中,需要格外注意某些相关的稳定性问题[168]。
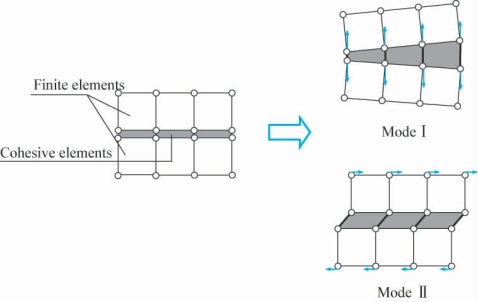
图4-5 内聚单元方法
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




