多尺度分析混凝土随机损伤本构理论的研究成果

实际的固体力学分析问题，数学上一般归结为偏微分方程的求解问题。经过了几十年的发展，对于固体力学分析中常见的偏微分方程，现代计算力学已经建立起了一套较为完整和固定的体系对其进行数值模拟。其基本的过程主要包含以下三步：第一是连续场的离散表示，通过插值函数的构造，将连续场表示为离散节点的数值；第二是代数方程的构造，将离散节点表示的连续场代入基本方程，经过一定的变换，将微分系统转化为代数系统；第三是代数系统的求解，求解由微分系统经过插值和变换得到的代数系统。对于后面两步，其过程和方法相对固定，不同的结构模拟方法的区别主要体现在第一步，即插值函数的构造。

对于结构的位移场，一般可以在构造一定的插值函数的基础上，将其统一表示为如下离散形式

其中，uh（x）为近似位移场，φI（x）为第I节点插值函数，dI为第I节点位移系数，NP为节点总数。

对于有限单元法，一般先基于单元定义节点之间的相互关系，再在单元内构造插值函数。单元之外的节点对于当前插值点没有影响，所以位移场插值式（4-97）可以采用单元的方式重新组织，转化为

其中，为插值点所在单元内的第I节点插值函数，ξ为广义坐标。

由于有限元法的插值函数满足克罗内克δ性质，所以节点的位移系数直接等于节点位移uI，NE N为单元节点数。

当然，也可以不利用网格，而是直接基于节点构造插值函数，由此建立起来的方法称为无网格方法［153-156］。这里以再生核粒子方法（reproducing kernel partial method）［155，157］为例，简要介绍一下无网格方法中插值函数的构造。首先引入多维多项式标识如下

RKPM的插值函数可表示为

式（4-102）中核函数φa（·）的覆盖半径（support size）为a，｛（xxI）α｝｜α｜≤n为分项基函数，而｛bα（x）｝｜α｜≤n分项基函数的系数函数，可以由再生条件（reproducing condition）

解得，表示为

此处H（x）=｛xα｝｜α｜≤n为所有的基函数组成的向量；而矩函数矩阵为

至此，可以求出再生核函数集合φI（x）作为微分方程求解的插值函数。另一方面，由于此时构造的再生核函数不再满足克罗内克δ性质，所以节点的位移系数并不一定等于节点位移。

虽然不同的方法构造的插值函数有很大的不同，但是各类插值函数却都满足某些共同的性质。Babuska［158］经过研究发现，各类方法构造的插值函数φI（x）往往满足单位分解条件（partition of unity），即

上式的物理意义是插值函数能够精确地表示常位移场。

Babuska［158］的研究发现，只需再附加极为宽松的条件，譬如方程的解能够用插值函数表示，那么上述单位分解条件（4-106）就可以保证结构分析的收敛。单位分解条件说明了两个方面的问题：其一是可以通过引入某些加强函数（enrichment）来描述通过常规方法构造的插值函数不能够很好描述的问题，如裂纹扩展问题；其二是为了保证结构分析的收敛，引入的加强函数（enrichment）不能破坏原来插值函数的单位分解性质。

对于位移场插值表达式（4-97），在单位分解的基础上引入加强函数gI（x）之后，可表示为［159］(https://www.xing528.com)

对于更加广泛的一类情况，如果引入NER个加强函数，那么位移场插值表达式为［159］

在有限单元法中采用单位分解方法引入加强函数，来求解某些包含间断面和奇异点的问题，就得到了扩展有限元法（extended finite element method）［160-162］的基本思路。对于裂缝扩展问题，对于求解区域划分有限元网格之后，其中的单元可以分为三类：第一类单元中不包含任何裂缝，这类单元的位移场是连续的，其插值函数可以采用有限元插值函数，不需要引入加强函数；第二类单元被裂缝贯穿，其位移场包含不连续，需要引入常规不连续函数作为加强函数；第三类单元，裂缝端部刚好进入单元内部，其位移场包含不连续，同时其应力-应变场还包含奇异点，需要引入非连续奇异函数作为加强函数。对于后两类单元，Moes and Belytschko［162］分别引入不同的加强函数。其中，对裂缝贯穿的单元，引入第二类Heaviside函数描述其不连续性质，即

对于第三类单元，即包含裂缝端部场的单元，须同时考虑不连续性和奇异性。对于线弹性断裂问题，一般采用线弹性断裂力学裂缝端部场的近场解来加强包含裂缝端部的有限单元的解，考虑裂缝端部近场解所包含的基函数，可采用如下一组加强函数［160，161］

其中（r，θ）为建立在裂纹端部的局部极坐标系，可以方便地转换到整体坐标系x中。对于内聚性裂纹问题，裂纹端部场不再奇异，Moes and Belytschko［162］建议根据内聚性裂纹模型的形式选取如下一种作为裂纹端部单元的加强函数。

最终可得裂缝问题的扩展有限元法（X-FEM）的插值表达式为

其中NP2与NP3分别为第二类单元和第三类单元所对应的节点集合，而

表示裂缝路径。式（4-112）称为X-FEM插值近似。

对于固体力学分析问题，根据略去体力的平衡方程以及边界条件，推导可得其等价弱形式。即寻找位移场解

使得泛函

恒成立。其中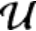为运动容许位移场，其数学结构与实际位移场的结构有关，若实际位移场连续，可取连续场，若实际位移场间断或者奇异，容许场也应该随做相应的改变。考虑小变形应变-位移关系与线性应力-应变关系，泛函式（4-115）化为

考虑到X-FEM插值表达式（4-112）之后，上式化为

其中近似解空间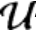h不但包含各个节点常规位移自由度｛aI｝，还包含加强函数所引入的广义自由度｛bJ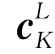，｝。后续的刚度矩阵组合求解等过程与常规有限元方法类似，只需注意加强函数引入的广义自由度即可。

上述加强函数方法的思路和过程不仅适用于对有限单元进行扩展，也可以直接应用于无网格方法等其他计算方法的拓展。

加强函数方法具有严格的数学基础（即单位分解条件），同时与有限元法以及无网格方法等通用数值方法能够很好地结合，所以一经提出就为多数研究者所接受，广泛应用于实际结构的分析中。另一方面，加强函数方法也存在一些应用层面的问题，譬如在引入了不连续加强函数后，整个系统的数值积分精度迅速降低，要想得到准确的结果，需要在加强函数附近引入特殊的积分项策略，这不仅会影响数值分析的效率，同时也会影响数值系统的收敛性和稳定性。