几何非线性引入的混凝土损伤本构理论研究

实际上，在基于散度定理的推导过程中，并没有引入材料性质，所以上述能量传递定义可以适用于基体中出现材料非线性的情况。另一方面，上面推导过程中，采用了线性的应变与位移关系，所以上述结论不能直接应用于几何非线性问题。当然，实际应用中，材料非线性与几何非线性往往是相互联系的，大的局部变形往往会引起材料非线性，而材料非线性引起的弱化和软化又往往导致局部变形的集中。所以本小节希望在多尺度能量传递定理中引入几何非线性的影响。

首先，考虑材料基体中出现非线性的情形。对于实际结构而言，非线性一经出现，往往倾向于集中到某一个区域，区域内部进入非线性，区域外部保持线性。本书也考虑此类非线性区域，并且引入隔离体的技巧，将非线性区域与线性基体隔离开来，如图4-2所示。图中考虑非线性区域Ωin，将非线性区域隔离出单元体Ωy之后，剩余部分基体为Ωm，同时隔离体交界面内力为p。

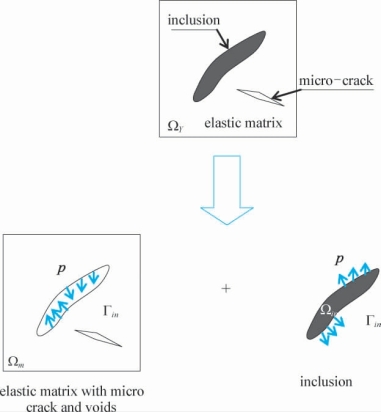
图4-2　细观基体中的非线性区域和隔离体

对于隔离出非线性区域之后剩余的基体部分，可以看作线性基体内部存在微裂缝微空洞的情形，应用多尺度能量传递定理，有

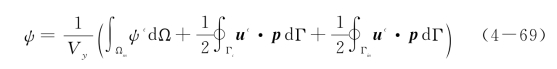
非线性带内的材料仍然可以采用连续介质力学的方法描述，但应当考虑材料及几何非线性。这样上式右边第三项中的闭合曲面积分可以用非线性带内的体积分表示，下面给出详细推导。

非线性带所占据的空间为Ωin，边界为Γin。考虑大变形引起的几何非线性之后。在初始坐标系Y内，非线性带的位型用表示；而在当前坐标系y内，非线性带的位型用表示。在连续介质力学中，在当前坐标系与初始坐标系之间可定义映射函数

材料点的位移定义为

在当前坐标系中，平衡方程一般基于柯西应力τ表达为

对应的外力边界条件，即非线性带隔离面上的应力作用，为

(www.xing528.com)

上述平衡方程两端乘以u∈并在单元体内做体积分，可得

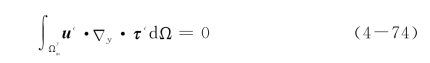
上式做分部积分，可解得式（4-69）中右边第三项面积分，有

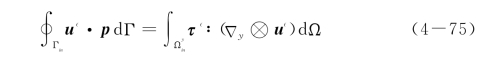
考虑到连续介质力学中对偶应力-应变的定义，还可以将上述积分表示成另外几个常用的形式，有

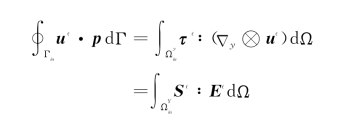
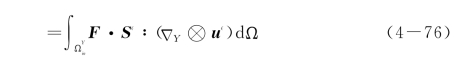
其中，F·S∈和S∈分别为第一类和第二类Piola-Kirchhoff应力；E为Green应变。至此我们推导得到了利用非线性带内应力-应变积分求解边界积分的方法。将上式代入式（4-69）后可以看出，整个多尺度能量积分还是分解为了两个部分：一部分是连续基体的体积分，其中包含线性部分和非线性部分；另一部分则是间断面的影响。引入拓展的细观Helmholtz自由能势如下：

其中Σ∈与Ξ∈为能量对偶应力和应变，可以根据具体情况取不同的表达式，只要满足连续介质力学中的能量对偶和等效即可，在线性小变形条件下，各类对偶应力-应变的定义都收敛到线性应力与应变表达式。

经过整理，可得推广的多尺度能量传递定理

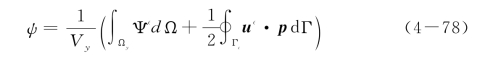
上述表达式可以同时考虑材料和几何非线性的影响。