数值模拟中，细观单元断裂应变的分布仍然采用前述抽象细观弹性-断裂模型中采用的对数正态分布，其密度函数和参数的表达式如式（3-22）、式（3-21）和式（3-20）。另一方面，由于对数正态分布的分布函数没有解析表达式，其计算需耗费一定的计算量，这里同时尝试采用Weibull分布作为对数正态分布的一种近似逼近。Weibull分布的密度函数为
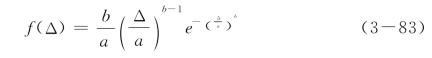
积分可得分布函数
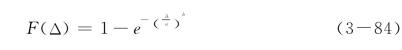
分布的均值和方差表达式为
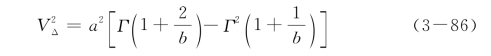
其中，Γ（·）为Gamma函数。
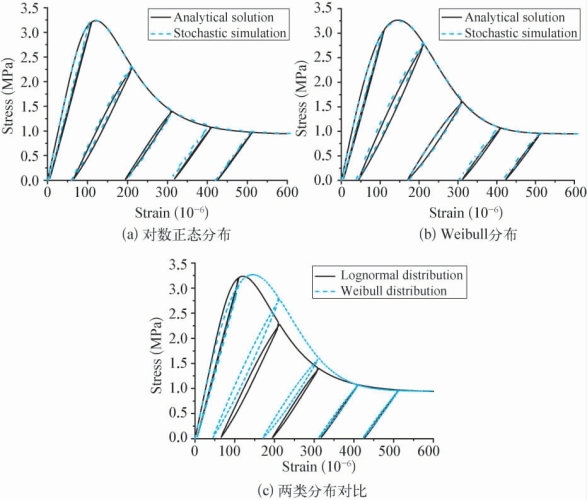
这里采用直接随机模拟方法，即直接模拟具有大量单元的并联系统，验证理论推导的正确性。将前述推导的理论结果（即式3-82）与直接随机模拟的结果进行对比，随机模拟中取10万个细观单元组成并联系统。数值模拟参数取：E0=37 559MPa，ηs=0.15，ηe=0.3，λ=5.0，ζ=0.45，a=190，b=2.0。由图3-21中的结果可以看出，直接随机模拟的结果与本书的解析结果非常吻合，验证了本书理论推导的正确性。同时采用本书的理论结果，其计算效率较之直接随机模拟有明显的提高。
(www.xing528.com)
图3-21 直接随机模拟与理论结果对比
应用Taylor［97］提到的混凝土单轴受拉重复加载试验。分别采用对数正态分布与Weibull分布模拟试验结果，所得理论结果与试验结果的对比如图3-22。实测试件的弹性模量为：E0=34 810MPa，模拟中，采用的对数正态分布计算参数为λ=5.0，ζ=0.35，ηs=0.09，ηe=0.25；Weibull分布的计算参数为a=180，b=2.4，ηs=0.09，ηe=0.20。
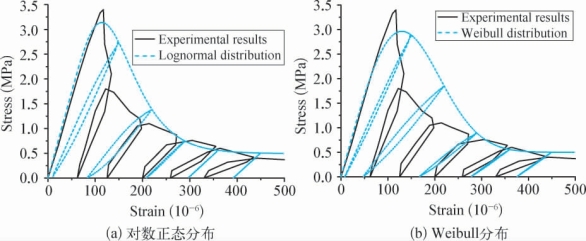
图3-22 单轴受拉重复加载结果
Karsan and Jirsa［96］进行了混凝土单轴受压重复加载试验。这里分别采用数正态分布与Weibull分布模拟实验结果。实测混凝土弹性模量E0=32 000MPa，对数正态分布的计算参数为λ=7.38，ζ=0.71，ηs=0.12，ηe=0.25；Weibull分布的计算参数为a=2 100，b=1.35，ηs=0.13，ηe=0.25。模型结果与试验结果的对比如图3-23。
由对比结果可以看出，本书模型能够同时描述混凝土在重复荷载作用下的损伤和滞回性能，并且计算简单，易于实现。另一方面，不论是单轴受拉结果还是单轴受压结果，对数正态分布得到的结果均更接近试验结果。
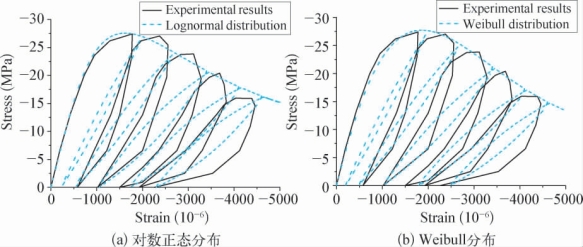
图3-23 单轴受压重复加载结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
