基于多尺度分析揭示混凝土滞回特征

为了便于分析，这里采用并联系统模拟单轴受力试件。对于细观单元而言，其性能可以划分为两个阶段：断裂前，单元保持弹性，其加载与卸载曲线均为直线；发生断裂时，单元的应力有瞬间跌落，但是并不跌落至0；断裂后，具有残余应力，同时由于内部裂缝表面摩擦的影响，加载与卸载曲线分离，具有滞回圈的性质。考虑到这种性能，我们建议了图3-15所示的细观单元。其中主弹性元件表征单元的弹性性能；断裂元件定义了单元的断裂应力σc；摩擦元件定义了单元的残余应力σs；次级弹性元件用于描述开裂后单元的弹性刚度。整个单元的性质由断裂单元控制，分为两个阶段，断裂前为弹性，断裂后为理想弹塑性。

先考虑单调加载情况下上述细观单元的行为。利用Heaviside函数，可以将两阶段的应力-应变关系统一表述为一个等式，有

其中Δ=σc／E0为断裂应变。

根据以往的实验研究［146，147］，断裂应力与残余应力之间，有如下线性关系

图3-15　细观单元的构成

其中，ηs为剪力保持因子。综合上面两式可得

单调加载条件下细观单元的应力-应变曲线如图3-16。

细观单元的卸载和再加载行为稍显复杂，如图3-17所示。

断裂前，卸载和再加载均沿着初始直线进行；断裂后，卸载与再加载表现出明显的滞回性能。滞回环水平段的应力的绝对值为残余应力σs，而卸载与再加载的刚度等于主弹性元件与次级弹性元件的串联刚度，为

图3-16　细观单元单调加载应力-应变曲线

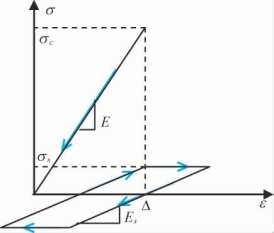
图3-17　细观单元卸载与再加载应力-应变曲线

其中，ηe定义为刚度折减系数。

定义（εmax，σmax）为单调加载曲线上的初始卸载点，那么整个细观单元的卸载曲线可以用下述分段函数表示

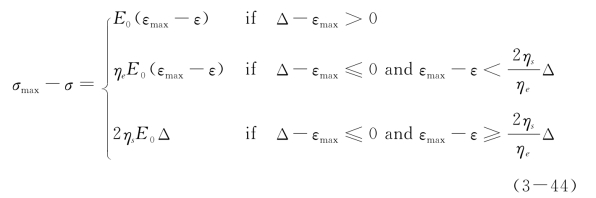
采用Heaviside函数，可以将上述分段函数整理在一个统一的表达式内，有

其中

由图3-17可以发现，不论是断裂前还是断裂后，卸载曲线与再加载曲线都是中心旋转对称的，同时再加载至初始卸载点之前，细观单元不会发生断裂。因此，再加载曲线可以由卸载曲线经过旋转对称变换直接得到。

定义再加载点为（εmin，σmin），则再加载过程的应力-应变曲线为

当再加载超过初始卸载点（εmax，σmax）时，再加载曲线回到单调加载曲线上。

下面讨论细观并联元件系统的求解。首先引入断裂-应变随机场Δ（x），同前述细观断裂模型一样，假定其一维密度函数和分布函数为

同时再定义期望函数

令

表示第i个细观单元的应力，xi为第i个单元的空间坐标，M为细观单元总数。考虑每个细观单元的截面积相同，那么整个并联系统的平均应力为

上式两端取极限M→∞，有

式（3-54）定义了细观应力与宏观应力的联系，即宏观应力是细观应力的直接平均。

考察并联单元系统，系统中的单元可分为两种，断裂的单元和未断裂的单元（图3-18），因此，可以将宏观应力分解为两项，一项是未断裂单元的贡献，另一项是断裂单元的贡献，即有

其中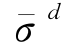，为未断裂部分的总应力；为断裂部分的残余应力。

考虑式（3-40），有

图3-18　并联系统的进一步分解

由于未断裂单元满足弹性性质，所以其应力可以用弹性应力-应变关系σ（xi）=E0ε代替，于是上式可化为

考虑极限M→∞，有

考虑随机损伤的定义式（3-3），可知上式中大括号内第二项即为随机损伤变量，于是上式化为

式中，为弹性有效应力。另一方面，对于并联系统断裂部分的残余应力，有

(www.xing528.com)

考虑极限M→∞，有

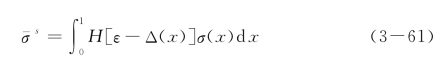
下面分两种情况讨论应力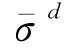与的表达式。

（1）单调加载段

对于单调加载的情况，断裂部分单元的应力直接等于残余应力，考虑式（3-61），有断裂部分的应力

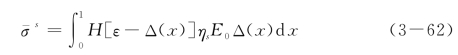
将式（3-62）与式（3-59）代入宏观应力式（3-55），可得

等式两边求数学期望，有

式（3-64）右边第一项

式（3-64）右边第二项

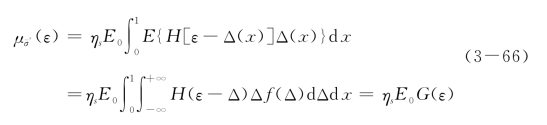
整理上述三式，可得单调加载下的应力应变演化的均值表达式为

由于本模型中建议的细观单元的性质比较复杂，所以尚难得到其方差表达式。在后面的求解中，将以求解均值应力为目的，并且认为应力的均值响应代表材料的宏观应力状态。

（2）卸载段和再加载段

将单元的卸载曲线式（3-45）代入宏观应力积分式（3-54），可得卸载段应力的表达式如下：

式（3-68）右端第一项

由上式可得卸载过程中未断裂部分的卸载应力

可知卸载过程中损伤d=d（εmax）保持不变。式（3-68）右端第一项的数学期望定义为Φ1，有

将式（3-69）代入式（3-68），可得

上式即为卸载段断裂部分单元承担的应力，两端作用期望算符，可得

两个积分号内的部分

卸载段应力-应变关系式（3-68）最终化为

其中函数Φ1，Φ2和Φ3的表达式分别见式（3-71）、式（3-76）和式（3-77）。定义抽象函数

那么卸载段平均应力-应变关系可以表示为

对于再加载段方程（3-49）重复上述推导过程，可得再加载段系统平均应力-应变关系

根据上述推导，可得系统的加载、卸载和再加载曲线如图3-19所示。当再加载越过初始卸载点（εmax，）时，应力-应变曲线就会折回到初始卸载曲线上，这从一个侧面体现了模型的“记忆性”，即模型会“记住”卸载点的位置，并且在对应点返回单调加载曲线。实际上，“记忆性”是本书推导的这一类模型与其他类型的滞回模型（如Bouc-Wen模型［148，149］）之间最大的区别。本书后面的讨论中将结合模型的滞回规则更细致地讨论“记忆性”的特点和影响。

图3-19　加载、卸载和再加载曲线

（3）滞回规则

在风、地震等非等幅重复荷载的作用下，结构往往表现出非常复杂的非线性行为。将非等幅重复荷载作用到上述损伤滞回模型上，也会得到一系列非常复杂的响应。Iwan［143］曾建议采用直接数值模拟得到并联滞回模型在非等幅荷载作用下的性能。这一思路虽然简单，但是需要追踪和记录每一个细观单元的加载历史和应力状态，同时为了得到连续性较好的模拟结果，所模拟的细观单元的数量又不宜过少，所以直接数值模拟的计算效率并不高。通过对系统的进一步分析，研究者［144］发现可以在加载、卸载和再加载曲线的基础上，引入一系列准则，来完整描述并联系统在非等幅荷载作用下的性能。对于Iwan模型，其对应的准则就是Masing准则。参照Ashrafi等人的工作［145］，本书建议如下两条准则：

（I）滞回环内。系统的损伤-滞回性能可以用下述表达式表示

其中，（ε＊，σ＊）为加载反转点。

（II）滞回环间。如果内环在卸载或者再加载过程中与外环曲线相交，那么后续的曲线将转入外环。

上述第一条滞回准则规定了前面求出的加载、卸载和再加载曲线是复杂重复荷载作用下系统滞回性能描述的基本元素。而第二条准则则精准地规定了系统的记忆性，即卸载至内圈时，需要记住外圈的卸载和反向加载点，一旦卸载或者反向加载至外圈，那么内圈的记忆就抹除。基于此，系统的记忆性可以由一个从大到小的序列描述，这一类记忆性称为序列记忆性或者离散记忆性［150］。离散记忆性与一般的塑性力学或者损伤力学中内变量描述的记忆性有着很大的区别：内变量在描述记忆性过程中，其个数和形式是不变的；而描述离散记忆性的序列，其长度是不断变化的，并且从理论上讲可以趋近于无穷。

根据上面两条滞回准则，所得复杂重复加载条件下的系统性能如图3-20所示。

图3-20　复杂重复加载条件下的损伤滞回性能